UNIVERSITY OF TORONTO
DEPARTMENT OF MATHEMATICS
MAT 237 Y - MULTIVARIABLE CALCULUS
FALL-WINTER 2005-06
ASSIGNMENT #1. SOLUTIONS
1. Compute the area of the surface generated when the parametric curve
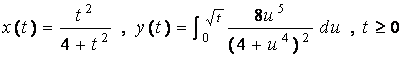 is rotated about the line x = 1 .
is rotated about the line x = 1 .
Solution:
Setting up the integral corresponding to this surface area we obtain:
A
= ![]() ,
where
,
where
1 x ( t ) =
![]() ,
x’
( t ) =
,
x’
( t ) = 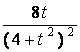 ,
y ’
( t ) =
,
y ’
( t ) =  ,
and
,
and
[ x’
( t ) ] 2 + [ y
’
( t ) ] 2 = 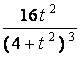 .
.
So, the area is A =
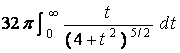 =
=
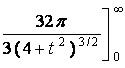 =
=
![]() .
.
2. Determine the maximum and minimum values of the curvature at points of the polar curve r = 3 + sin q .
Solution.
The given curve can be parametrized as:
x(q
) = rcosq
= 3cosq
+ sinq
cosq
= 3cosq
+ ![]() sin(2q
) , and
sin(2q
) , and
y(q
) = rsinq
= 3sinq
+ sin 2q
= 3sinq
+ ![]() (1
cos(2q
)) , 0≤q
≤2p
.
(1
cos(2q
)) , 0≤q
≤2p
.
Now, x’(q ) = 3sinq + cos(2q ) , y ’(q ) = 3 cosq + sin(2q ) ,
x²(q ) = 3cosq 2sin(2q ) , y ²(q ) = 3sinq + 2cos(2q ) ,
x’(q ) y ²(q )x²(q ) y ’(q )=11+9(sin(2q )cosq sinq cos(2q ))=11+9sinq , and
[x’(q )] 2 + [y ’(q )] 2 =10+6(sin(2q )cosq sinq cos(2q ))=10+6sinq .
Therefore, K (q
) =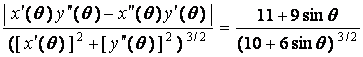
and K
’(q
) =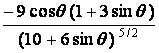 .
.
The possible extrema of K (q ) are at q = 0, p /2, 3p /2, arcsin(1/3) .
Testing, we find K(0)=11/103/2 » 0.3479 , K(p /2)=20/163/2 = 0.3125 ,
K(3p
/2)=2/43/2 =![]() and
K(arcsin(1/3))=8/83/2=
and
K(arcsin(1/3))=8/83/2=![]() »
0.3536 .
»
0.3536 .
So, the
minimum and maximum curvatures are
![]() and
and
![]() ,
respectively.
,
respectively.
3.
Let p denote a real number such that 0 < p < 1 and
let v 1 , v 2 , v 3 ,
be vectors in
R3
such that
![]() and
and
![]() for
all k = 1 , 2 , 3 ,
Find the values of p , if any,
for which
for
all k = 1 , 2 , 3 ,
Find the values of p , if any,
for which
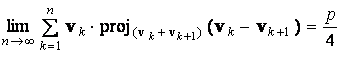 .
.
Solution.
Notice that 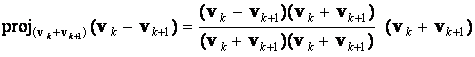
=
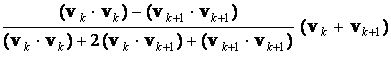
=
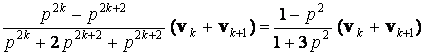 ,
and
,
and
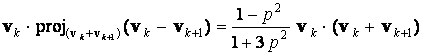
=
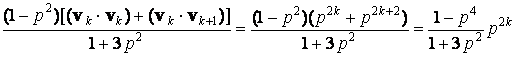 .
.
Now,
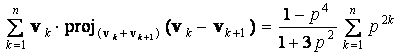
=
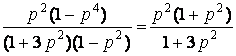 .
.
We want to find the values of 0 < p < 1 such that 4 p 3 3 p 2 + 4 p 1 = 0 .
The polynomial function f ( p ) = 4 p 3 3 p 2 + 4 p 1 is continuous and differentiable
everywhere. The function f has at least one zero over ( 0 , 1 ) because f ( 0 ) = 1 and
f ( 1 ) = 4 . That is the only real zero of f because f ’ ( p ) = 12 p 2 6 p + 4 > 0 for all p .
So, there is a unique value of p . An approximated value is p » 0.2884 .
4. Prove or disprove each of the following propositions:
a) If
C 1 , C 2
, C 3 ,
are all closed sets in R n
, then the set
 is
also a closed set in R n .
is
also a closed set in R n .
Solution:
This proposition is false. We will give a counterexample.
Consider the sets C 1 = { 1 } , C 2 = { 1 / 2 } , , C k = { 1 / k } ,
All of these sets are obviously closed but their union
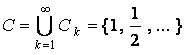 is not a closed set because
is not a closed set because ![]() implies
that 0 is a boundary
implies
that 0 is a boundary
point of C and 0 Ο C .
b)
If A 1 ,
A 2 , A 3 ,
are all non empty compact
sets in R n such that A k
+ 1
Μ A
k
for all k = 1 , 2
, 3 ,
, then the set
 is
also non empty.
is
also non empty.
Solution:
This proposition is true.
We will prove that the assumption A is an empty set leads to a contradiction.
Notice that all the sets A
k are closed because they are compact. Therefore, the sets
![]() are
all open. Assume now that the set A is empty. If the set A
is empty then
are
all open. Assume now that the set A is empty. If the set A
is empty then
 .
It means that
.
It means that ![]() is
an open cover of R n and
is
an open cover of R n and
therefore an open cover
of A 1
Μ
R n . Consider now any finite choice of some of
these open sets, say ![]() where
k 1 < k 2 < k 3 <
<
k m . Notice that
where
k 1 < k 2 < k 3 <
<
k m . Notice that
![]() because
because
![]() therefore
therefore
![]() but
but
![]() because
Ζ
Ή
because
Ζ
Ή
![]() Μ
A 1 .
Μ
A 1 .
So
![]() is
an open cover of A 1 that does not contain a finite
subcollection of open sets which also covers A 1 . This
is a contradiction because A 1 is a compact set.
is
an open cover of A 1 that does not contain a finite
subcollection of open sets which also covers A 1 . This
is a contradiction because A 1 is a compact set.
|
HOME |
|