UNIVERSITY OF TORONTO
DEPARTMENT OF MATHEMATICS
MAT 237 Y - MULTIVARIABLE CALCULUS
FALL-WINTER 2005-06
ASSIGNMENT #1. DUE ON OCTOBER 6
PROBLEMS
DO NOT SUBMIT YOUR SOLUTIONS WITHOUT THE COVER PAGE.
READ THE INSTRUCTIONS WRITTEN ON THAT PAGE.
1. Compute the area of the surface generated when the parametric curve
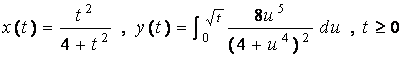is rotated about the line x = 1 .
2. Determine the maximum and minimum values of the curvature at points of the polar curve r = 3 + sin q .
3. Let p denote a real number such that 0 < p < 1 and
let v 1 , v 2 , v 3 ,
… be vectors in R 3 such that
and
for
all k = 1 , 2 , 3 , … Find the values of p , if any,
for which
.
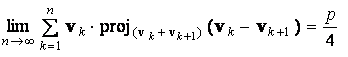4. Prove or disprove each of the following propositions:
a) If
C 1 , C 2
, C 3 , … are all closed sets in R n
, then the set
is
also a closed set in R n .
b)
If A 1 ,
A 2 , A 3 , … are all non empty compact
sets in R n such that A k
+ 1
Ì A
k for all k = 1 , 2
, 3 , … , then the set
is
also non empty.
|
• HOME |