Geometry of the Plane
Worked Examples
Parabolas
The formula for a parabola with vertex $(h,k)$ is $$ y-k = a(x-h)^2. $$
Example.
Find the equation of a parabola that passes through the points $(0,3)$, $(1,6)$, and $(3,6)$.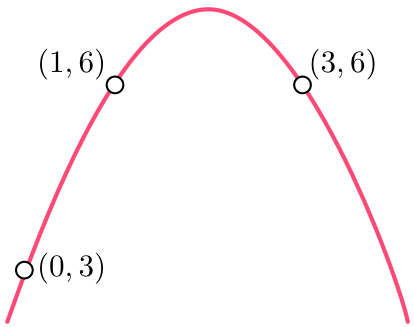
We plug in these values in the formula as the $x$ and $y$ values: \begin{align} 3-k & = a(0-h)^2 \\ 6-k & = a(1-h)^2 \\ 6-k & = a(3-h)^2 \end{align} We now solve this (nonlinear) system of 3 equations to 3 unknowns.
Setting the two last equations equal to each other: $$ (1-h)^2 = (3-h)^2, $$ so $1-h = \pm(3-h)$, which implies that $h=2$. (Details) So $$ 1-h = \pm (3-h) $$ which implies that either $$ 1-h = 3-h \; , \quad \text{thus } \; 1=3 $$ (which is FALSE), or $$ 1-h = -(3-h) \; , \quad \text{so } \; h=2. $$ We deduce that $h=2$.
Let us rewrite all 3 equations: \begin{align} 3-k & = 4a \\ 6-k & = a \\ 6-k & = a \end{align} Since the last 2 equations are equal, we can disregard one of them.
From the first two equations, we solve for $k$: \begin{align} k & = 3-4a \\ k & = 6-a \end{align} so $3-4a=6-a$, which implies that $a=-1$, thus $k=6-a = 7$.
The equation of the parabola that passes through these 3 points is: $$ y-7=-(x-2)^2. $$ It has vertex at $(2,7)$ and is turned downwards ($a<0$).
