Geometry of the Plane
Worked Examples
Quadrilaterals
There are several kinds of quadrilaterals. We can identify them by their vertices and slopes.Rectangles are quadrilaterals containing ony right angles. If the sides have equal lengths, then it is called a square.
We can check that we have a rectangle by checking the slopes of the sides: they are parallel or perpendicular.
Parallelogram are quadrilaterals with opposite sides parallel. If the sides have equal lengths, then it is called a rhombus.

Trapezoid are quadrilaterals where one pair of opposite sides are parallel

Example.
Move the points $A$, $B$, $C$, and $D$ to obtain different quadrilaterals.Example.
What kind of quadrilateral has the following vertices: $(0,5)$, $(1,2)$, $(4,8)$, and $(5,5)$.Solution. First we draw these four points:
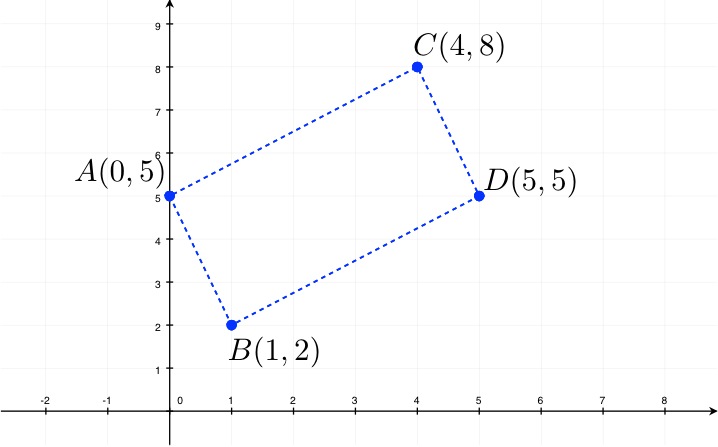
We now check the slopes of the sides of the quadrilateral: \begin{align} \text{slope of } AB & = \frac{2-5}{1-0} = -3 \\ \text{slope of } BD & = \frac{5-2}{5-1} = \frac34 \\ \text{slope of } AC & = \frac{8-5}{4-0} = \frac34 \\ \text{slope of } CD & = \frac{5-8}{5-4} = -3 \end{align} Observe that adjacent sides ($AB$ and $BD$) are not perpendicular (Details)Try to show why they are not perpendicular, so it is not a rectangle or a square.
Also, we have two pairs of parallel sides: $AB$ is parallel to $CD$, and $BD$ is parallel to $AC$.
So it is a parallelogram or a rhombus.
To distinguish between them, we need to check the length of the sides: \begin{align} {\rm distance}(A,B) & = \sqrt{(2-5)^2+(1-0)^2} = \sqrt{10} \\ {\rm distance}(B,D) & = \sqrt{(5-2)^2+(5-1)^2} = 5 \end{align} (Details)The distance formula will be reviewed in the next page (Other Formulas)
Since the length of the sides are not equal, the quadrilateral is a parallelogram.
