Graphing

Ellipses

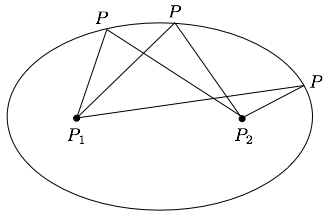
An ellipse is a generalization of a circle.

Recall that a circle is determined by its centre and radius, $r$, it is the set of all points at distance $r$ from the centre. An ellipse is determined by two points, $P_1$ and $P_2$, the foci, and a distance $d$. It is the set of points $P$ such that $dist(P,P_1)+dist(P,P_2)=d$. (See the Geometry section on distances between two points.)



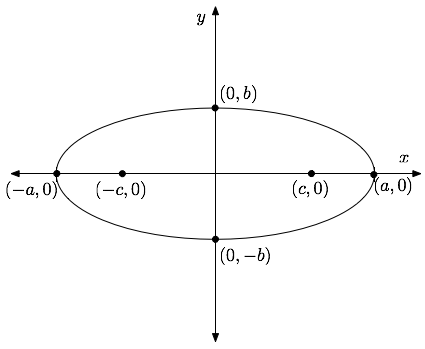
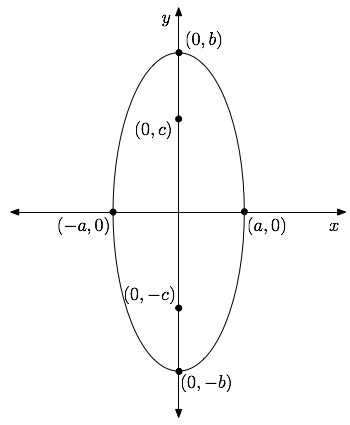
The standard form for the equation of an ellipse centered at the origin and aligned with the axes is: $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad (a>0, b>0) $$ The larger of $2a$ and $2b$ is the length of the major axis of the ellipse, and the smaller is the length of the minor axis. The foci are obtained by computing $c^2=|a^2-b^2|$ and are given by: $$\left\{ \begin{array}{ l r } (\pm c, 0) & if \;\; a>b \\ (0,\pm c) & if \;\; a < b \\ \end{array} \right.$$

The graphs for the two cases are illustrated below.
To graph an ellipse, given the standard equation, we can solve for $y$: $$y = \pm b\sqrt{1-\frac{x^2}{a^2}}$$ Taking the right side with a positive sign gives the upper half of the ellipse, and taking it with a negative sign gives the lower half.

Example.

Solution: The ellipse $\frac{x^2}{16}+\frac{y^2}{25}=1$ is elongated in the $y$-direction, the major axis extending from $(0,-5)$ to $(0,5)$ and the minor axis, from $(-4,0)$ to $(4,0)$. To graph it, we solve for $y$: $$y = \pm 5 \sqrt{1-\frac{x^2}{16}}$$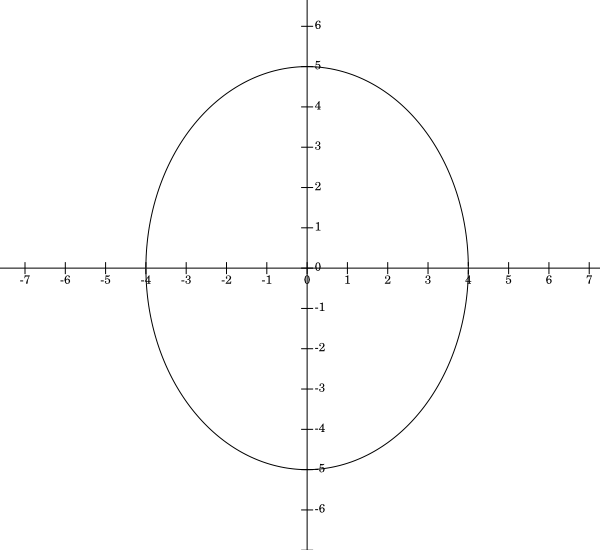

Example. Find the foci of the ellipse $4x^2+25y^2=100$.

Solution: The standard form equation is $\frac{x^2}{25}+\frac{y^2}{4}=1$.

We compute $c^2=|25-4|=21$.

Since $25 > 4$, the ellipse is elongated in the $x$-direction and the foci are on the $x$-axis, given by $(\pm \sqrt{21}, 0)$.

Example. Find the equation of the ellipse which has foci $(\pm 3,0)$ and major axis extending from $(-4,0)$ to $(4,0)$.

Solution: We're given the major axis is on the $x$-axis so in the standard ellipse equation, we get $a=4$ and $a > b$.

To get $b$, we observe that $c=3$ and from $c^2=a^2-b^2$, we get $9=16-b^2$, so $b^2=7$ or $b=\sqrt{7}$.

The equation of the ellipse is $\frac{x^2}{16}+\frac{y^2}{7}=1$.