Graphing
Worked Examples
Circles
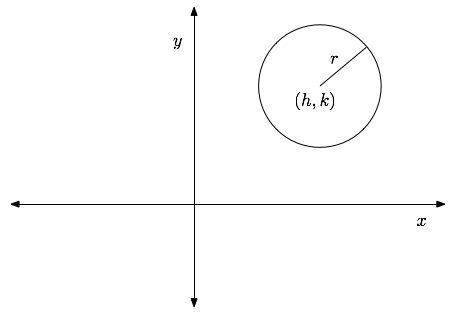
In this and the following three sections, we will discuss how to graph conic sections, i.e. curves obtained from the intersection of a cone with a plane, including circles, ellipses, hyperbolas and parabolas.A circle with radius $r$ centered at the point $(h,k)$ has the following equation:
$$(x-h)^2+(y-k)^2=r^2$$ This is the standard form for the equation of a circle.
Example.
The circle with equation $(x-7)^2+(y+4)^2=45$ has centre $(7,-4)$ and radius $\sqrt{45}=3\sqrt{5}$.If we have an equation of a circle not in standard form, we can turn it into standard form by:
| 1. | simplifying |
| 2. | factoring |
| 3. | completing the square (See the section on parabolas for more information.) |
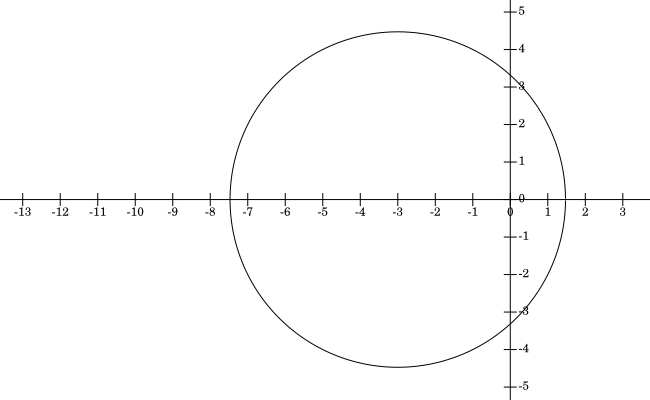
Example. Write the equation $x^2+y^2+6x-2y=10$ in standard form and graph the corresponding circle.
| $(x^2+6x)+(y^2-2y)$ | $=10$ | (Details)Group the $x$ terms and $y$ terms together. | |
| $(x^2+6x+9-9)+(y^2-2y+1-1)$ | $=10$ | (Details) Complete the square for $x$ and for $y$. | |
| $(x^2+6x+9)-9+(y^2-2y+1)-1$ | $=10$ | (Details)Leave the perfect square expressions in the brackets and take out the other terms. | |
| $(x+3)^2 + (y-1)^2$ | $=10+9+1$ | (Details)Bring the numbers outside the brackets to the right and factor the left side. | |
| $(x+3)^2 + (y-1)^2$ | $=20$ | (Details)Simplify. |
Hence, the standard form is $(x+3)^2 + (y-1)^2 = 20$ and we have a circle of radius $\sqrt{20}=2\sqrt{5}$ centered at $(-3,1)$. The graph of the circle is: