Functions and Their Inverses
Worked Examples
Exponential and Logarithmic Functions
Part 1. Exponential Functions
The exponential function with base $b$ is defined for $x \in \mathbb{R}$ by $f(x) = b^x,$ where $b > 0$ and $b \neq 1.$Graphically, we can see the following properties:
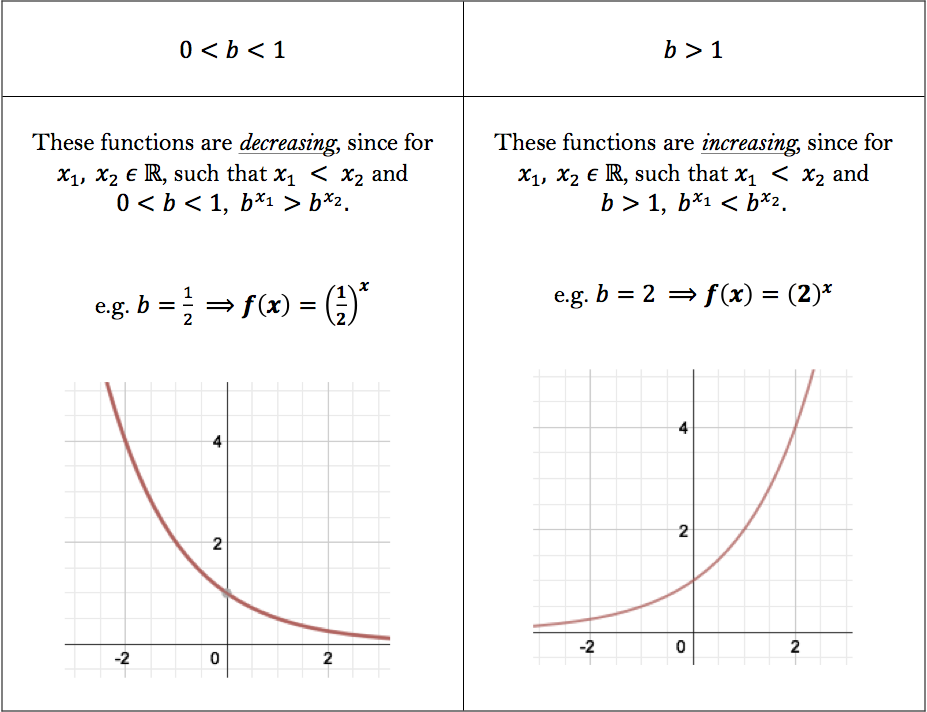
 Furthermore, because $b > 0$ (by definition), we know that $f(x) = b^x \neq 0$ for any $x \in \mathbb{R}.$ Consequently, we have a horizontal asymptote at the line $y=0.$
Definition: the line $y=c$ is a horizontal asymptote if as $x \to \pm \infty, \; f(x)\to c.$
The above properties of increasing and decreasing show that exponential functions are $1-1,$ and therefore have inverses (which will be discussed in Part 2).
 The natural exponential function is known as $y=e^x,$ where $e$ is Euler’s irrational number: $2.71828\cdots$
Note: For exponential functions, all the definitions and properties of exponents are applicable!
Example. Solve the following exponential equations:
| 1. | $2^x4^{3x+1} = \frac{2}{\sqrt{8}} $ |
| Solution: One strategy is to express both sides in terms of the same base, namely $b=2,$ so that the properties of exponents can be used.
\begin{align*}
& 2^x (2^2)^{3x+1} = \frac{2}{(2^3)^{1/2}} \\
& \Rightarrow 2^{x+6x+2} = 2^{1-(3/2)} \\
& \Rightarrow 2^{7x+2} = 2^{-(1/2)}
\end{align*}
Now, we have that $f(7x+2) = f\left( -\frac{1}{2} \right),$ where $f(x) = 2^x,$ and because exponential functions are $1-1,$ we can conclude that $7x+2 = -\frac{1}{2}.$
Therefore, $x = -\frac{5}{14}.$ |
|
| 2. | $ 3x(e^x) + x^2 (e^x) = 0 $ |
| Solution. First notice that $x\cdot e^x$ is a common factor. \begin{align*} (x)(e^x)(3+x) = 0 \Rightarrow x=0, \; e^x = 0, \; or \; 3+x = 0. \end{align*} But $e^x \neq 0$ for any $x \in \mathbb{R}.$ Consequently, the second equation yields no solution. Therefore, our only solutions are $x=0$ and $x=-3.$ | |
| 3. | $ 5^{2x}=3 $ |
| Solution. Here, we cannot use the strategy applied above, since there is no common base between $5$ and $3.$ So, we will now explore the inverses of exponential functions, which will present us with a strategy to solve such problems! |
Part 2. Logarithmic Functions (the inverses of exponential functions!)
Let $b$ be a positive number such that $b \neq 1.$ The logarithmic function with base $b,$ denoted by $\log_b$ is defined by: $$ \log_b(x) = y \Leftrightarrow b^y = x$$ $\log_b(x)$ reads "log base $b$ of $x$"
In other words:
$\log_b x= $ "the exponent $(y)$ that we raise the base $b$ to in order to obtain $x$"
Exercise. Find $\log_2 8$
\begin{align*} \log_2 8 = k & \Leftrightarrow 2^k = 8 \\ & \Leftrightarrow k = \log_2 8 = 3. \end{align*}Note: $f(x) =\log_b x$ and $g(x)= b^x$ are inverses!
Notice that in order to be inverses, the logarithmic and exponential functions must have the same base $b$!
We will verify that $f(x) = \log_b x$ and $g(x)=b^x$ are inverses by using the Cancellation Property:
\begin{align*} f(g(x)) &= \log_b(g(x)) \\ &= \log_b(b^x) \\ &= x \\ & \quad since \; \log_b(b^x) = k \Leftrightarrow b^k = b^x \Leftrightarrow k=x \\ & \quad \textrm{ (by the 1-1 property)} \end{align*} Similarly, \begin{align*} g(f(x)) &= b^{\left( f(x) \right)} \\ &= b^{\log_b x} \\ &= x \end{align*} since $\log_b(x) = $ "the exponent such that when $b$ is raised to it, it returns the value $x$" by definition.
i.e. $\log_b(x) = k \Leftrightarrow b^{\log_b x} = b^k =x.$
Graphically, we can see that they are inverses because the functions reflect about the line $y=x.$ Consider $f(x)= \log_2(x)$ (in blue) and $g(x)=2^x$ (in red), whose graphs are given below:
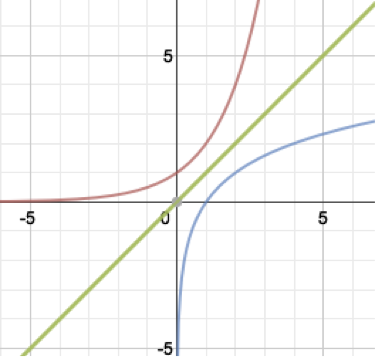
Notice that the domain of $y=b^x$ is the entire real line, which is now the range of $y= \log_b x.$ Similarly, the range of $y =b^x$ is equal to the domain of $y = \log_b x,$ which is the interval $(0,\infty).$ This shows that while $y=0$ was a horizontal asymptote for $g(x)=b^x, \; x=0$ is now a vertical asymptote for $f(x)=\log_b x.$
Definition: the line $x=c$ is a vertical asymptote if as $x \to c, \; f(x)\to \pm \infty.$
Part 3. Two Important Logarithms
| 1. | $b=10$ |
| We usually write $\log x$ to mean $\log_{10} x.$ (i.e. the convention is to not write the base of ten) | |
| 2. | $b=e$ |
| We usually write $\ln x$ to mean $\log_e x.$ "$\ln$" stands for "natural logarithm" (so try not to say it like "lawn", though many do) |
Part 3. Properties of Logarithms
| i. | $\log_b b^x = x $ |
| ii. | $ log_b 1 =0 $ |
| iii. | $log_b b = 1 $ |
In summary, we have that: $$ \underbrace{log_br =s}_{\text{logarithmic form}} \qquad \qquad means \qquad \qquad \underbrace{b^s=r}_{\text{exponential form}}$$ Recall the basic properties of functions of the form $y=b^x$, where $b$ is a constant positive real number:
| 1. | $ b^r \cdot b^s = b^{r+s} $ |
| 2. | $ b^r \div b^s = b^{r-s} $ |
| 3. | $(b^r)^s = b^{rs} $ |
| 1. | $ \log_b(r\cdot s) = \log_b r + \log_b s $ |
| 2. | $ \log_b(\frac{r}{s}) = \log_b r - \log_b s $ |
| 3. | $\log_b(r) = \frac{\log_s r}{\log_s b}\qquad $ ("change of base" formula) |
Below is the proof of (1). The rest will be left to you as an exercise!
Proof of (1):
Call $x=\log_b r,$ $y=\log_b s,$ and $z = \log_b(r\cdot s).$ We need to show that $z=x+y.$
Well, by definition of logarithms, we have the following: \begin{align*} x &= \log_b r \Leftrightarrow b^x = r \\ y &= \log_b s \Leftrightarrow b^y = s \\ z &= \log_b(r\cdot s) \Leftrightarrow b^z = r\cdot s. \end{align*} Therefore, $b^z = r\cdot s = b^x b^y = b^{x+y} \;$ (by property 1 of exponents above)
$\Rightarrow b^z = b^{x+y} $
$\Rightarrow z = x+y\; $ (by $1-1$ property of exponential functions)
$\Rightarrow \log_b(r\cdot s) = \log_b r + \log_b s \;$ as desired.
Q.E.D.
Mini-Lecture.
Below is a mini lecture about exponentials and logarithms.
Example. Solve the following equations for $x$:
| 1. | $ 5^{2x} = 3 \;$ (from first example, #3, revisited) |
| Solution: Our goal is to solve for $x$, which is an exponent at the moment. So, in order to get our hands at the exponent, we simply apply the inverse of the exponential function with a base of $5$ (i.e. $\log_5 x$) to both sides. This will allow us to use the property $\log_b b^x = x.$ $$\log_5(5^{2x}) = \log_5(3) $$ This gives $2x = \log_5(3)$ Finally, we have: $x=\frac{\log_5(3)}{2}$ (which cannot be simplified further without a calculator!) | |
| 2. | $ 4 (1+10^{5x}) = 404 $ |
| Solution. A common approach is to first isolate the exponential function. \begin{align*} 4(1+10^{5x}) = 404 &\Rightarrow 1+10^{5x} = \frac{404}{4} \\ &\Rightarrow 1+10^{5x} = 101 \\ &\Rightarrow 10^{5x} = 100 \end{align*} Now, we can either express both sides of the equation using the same base, or apply the inverse of the exponential function to both sides. Let's proceed using the first option, since the same base of $10$ seems fairly obvious. \begin{align*} 10^{5x}=10^2 &\Rightarrow 5x = 2 \; \text{ by 1-1 property} \\ &\Rightarrow x = \frac{2}{5} \end{align*} | |
| 3. | $ e^x - 12 \cdot e^{-x} - 1 = 0 $ |
| Solution: This is simply a quadratic in disguise, which is revealed when we multiply both sides by $e^x$ (to cancel with $e^{-x}$). \begin{align*} e^x - 12 \cdot e^{-x} - 1 = 0 \Rightarrow e^x(e^x) - 12 \cdot e^{-x}(e^x) - 1(e^x) = 0(e^x) \\ &\Rightarrow (e^x)^2 - 12\cdot e^0 - e^x = 0 \\ &\Rightarrow (e^x)^2 - e^x - 12 = 0 \end{align*} Here is our quadratic! If this is still unclear, simply let $z = e^x$. So, our equivalent equation is given by: $(z)^2 - z - 12 = 0.$ This can be factored as follows: $$z^2 - z - 12 = (z-4)(z+3) = 0,$$ which gives that $z=4$ or $z=-3.$ Now we express everything in terms of $x$ in order to solve the desired equation. We have $$e^x = 4 \text{ or } e^x=-3 \; \text{ which isn't true for any x!}$$ So, there is only one valid solution, which we find by applying $\ln()$ to both sides of $e^x = 4:$ $$\ln(e^x) = \ln(4) \Rightarrow x = \ln(4).$$ | |
| 4. | $ \log_3(x+29) - 2 \log_3 (x-1)=0 $ |
| Solution: We first notice that the logarithms have the same base, so our Properties of Logarithms are applicable.
Using the $3$rd property (which allows us to "bring exponents up or down") yields the following equivalent equation:
$$ \log_3(x+29) - \log_3((x-1)^2) = 0.$$
Now we can use the $2$nd property, which gives:
$$\log_3\left( \frac{x+29}{(x-1)^2} \right) = 0.$$
The definition of logarithms states:
$$ \log_3\left( \frac{x+29}{(x-1)^2} \right) = 0 \Leftrightarrow 3^0 = \frac{x+29}{(x-1)^2}.$$
Consequently, we simply need to solve the following quadratic:
\begin{align*}
1\cdot (x-1)^2 = x+29 &\Rightarrow x^2 - 2x +1 = x+29 \\
&\Rightarrow x^2 - 3x -28 = 0\\
&\Rightarrow (x-7)(x+4) = 0 \\
&\Rightarrow x = 7 \text{ or } x = -4.
\end{align*}
Note: we must recall that logarithmic functions have restrictions on their domains.
Therefore, before declaring our final solutions, we must check that the $x$-values don't violate the domains of the original logarithmic functions.
Substituting back into the original problem, we have:
For $x= 7:$ We show: LHS (left hand side) = RHS (right hand side) of the original equation. $$\text{LHS } = \log_3 (7+29) - 2 \log_3 (7-1) = \log_3 \left( \frac{36}{6^2} \right) = \log_3 ( 1) = 0 = \text{ RHS}.$$ The important thing to note is that when we first substituted $x=7,$ both logarithmic functions were defined! For $x=-4:$ $$\text{LHS } = \log_3 (-4 +29) - 2 \log_3 (-4-1) = \log_3 \left( 25 \right) - 2 \log_3 ( -5).$$ But $\log_3(-5)$ is undefined! Therefore, $x=-4$ is not a valid solution! So $x=7$ is the only solution. |
