Functions and Their Inverses
Worked Examples
Introduction to Functions and Function Notation
Part 1. What is a Function?
A function $(f)$ is just a rule that relates two sets ($A$ and $B$), such that every element in $A$ is connected to at most one element in $B.$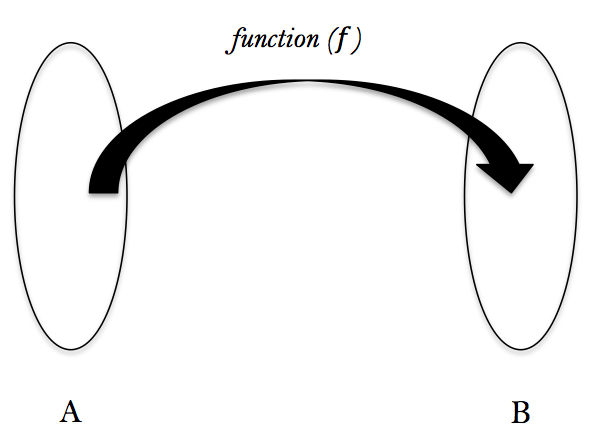
The domain of a function $f$ is the set $A$, of all the values that the function can act on. (i.e. the input)
The range of a function $f$ is the set $B$ of all the values returned by the function after it acts on the domain. (i.e. the output)
Because functions are just rules, we can express them in different ways:
| 1. | Verbally (a description) | ||||||||||
| e.g. Take a real number, subtract $3$, and then take the square root of the result. | |||||||||||
| 2. | Algebraically (by formula) | ||||||||||
| e.g.  $\sqrt{x− 3}$, where 𝑥 denotes any real number for which the expression is defined. | |||||||||||
| 3. | Numerically (using a table of values) | ||||||||||
|
|||||||||||
| 4. | Graphically (using Cartesian coordinates) | ||||||||||
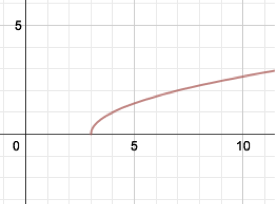 |
Remember: $f$ cannot take one value in $A$ and return more than one value in $B$!
You can determine if a graph represents a function by using the Vertical Line Test, which states:
A graph represents a function if and only if every vertical line intersects the graph at most once.
Let’s consider $y=\sqrt{x-3}$, whose graph was given above. We know it’s a function because for every vertical line $x=c$, the line intersects the graph at one point: $(c, \sqrt{c-3}).$
For example, the line $x=4$ only intersects the graph once, at the point $(4, 1 ).$ See the graph below.
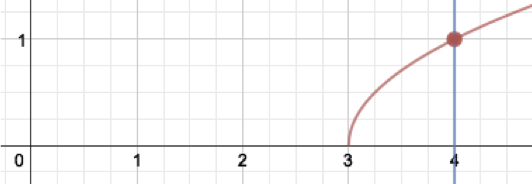
Part 2. Function Notation
Given a function $f$ and some number $x$,$f(x)$ represents the actual value of the function after the rule is applied to $x$, and reads “$f\;$ of $\;x$" , “$f\;$ at $\;x$", or “$f\;$ evaluated at $\;x$". Graphically, $f(x)=y$ since $y$ depends on $x$.
This is called function notation.
Exercise.
| 1. | Express each rule using function notation: |
| a) Take a number, add $1$, and then square the result. | |
| Solution: $ \qquad f(x) = (x+1)^2$ | |
| b) Take the $3$rd-root of a number, subtract $\; 2$, and then divide the result by the original number. | |
| Solution. $$g(x) = \frac{(\sqrt[3]{x})-2}{x}$$ | |
| 2. | Evaluate and simplify each function at the values indicated: |
| a) $h(x) = \frac{2\sqrt{x+4}}{|1-x|}$; $\qquad h(-3), \; h(0), \; h(8),\; h(a-1), \; h(x^2+4x)$ | |
| Solution: \begin{align*}h(-3) &= \frac{2\sqrt{(-3)+4}}{|1-(-3)|} \\ &= \frac{2\sqrt{1}}{|4|} \\ &= \frac{2}{4}\\ &= \frac{1}{2} \end{align*} | |
| $h(0) = $ Solution. \begin{align*} &= \frac{2\sqrt{(0)+4}}{|1-(0)|} \\ &= \frac{2\sqrt{4}}{|1|} \\ &= 2(2)\\ &= 4 \end{align*} | |
| $h(8) = $ Solution. \begin{align*} &= \frac{2\sqrt{(8)+4}}{|1-(8)|} \\ &= \frac{2\sqrt{12}}{|-7|} \\ &= \frac{2(2\sqrt{3})}{7}\\ &= \frac{4\sqrt{3}}{7} \end{align*} | |
| $h(a-1) = $ Solution. \begin{align*} &= \frac{2\sqrt{(a-1)+4}}{|1-(a-1)|} \\ &= \frac{2\sqrt{a+3}}{|2-a|} \end{align*} | |
| $h(x^2+4x) = $ Solution. \begin{align*} &= \frac{2\sqrt{(x^2+4x)+4}}{|1-(x^2+4x)|} \\ &= \frac{2\sqrt{(x+2)^2}}{|1-x^2-4x|} \\ &= \frac{2|x+2|}{|1-x^2-4x|} \end{align*} | |
| b) $$k(x) = \left\{ \begin{array}{llr} \sqrt[3]{x} & \textrm{ if }\; x \leq -1 & \\ 3-x^2 & \textrm{ if }\; -1 < x \leq 1 & (k(x) \text{ is called a piecewise function})\\ 2 & \textrm{ if }\; x > 1 & \end{array} \right.$$ $k(1), \; k(-8), \; k(25), \; k\left( -\frac{1}{2} \right), \; k(-1)$ | |
| Solution: For $x=1$, $k(x)=3-x^2$ by definition. \begin{align*}\Rightarrow k(1) &= 3-(1)^2 \\ &= 3-1 \\ &= 2 \end{align*} | |
| $k(-8) = $ Solution. For $x=-8$, $k(x)=\sqrt[3]{x}$ by definition. \begin{align*}\Rightarrow k(-8) &= \sqrt[3]{-8} \\ &= -2 \end{align*} | |
| $k(25) = $ Solution. For $x=25$, $k(x)=2$ by definition. \begin{align*}\Rightarrow k(25) = 2 \end{align*} | |
| $k\left(-\frac{1}{2}\right) = $ Solution. For $x=-\frac{1}{2}$, $k(x)=3-x^2$ by definition. \begin{align*}\Rightarrow k\left(-\frac{1}{2}\right) &= 3-\left(-\frac{1}{2} \right)^2 \\ &= 3-\frac{1}{4}\\ &= \frac{12}{4}-\frac{1}{4}\\ &= \frac{11}{4} \end{align*} | |
| $k(-1) = $ Solution. For $x=-1$, $k(x)=\sqrt[3]{x}$ by definition. \begin{align*}\Rightarrow k(-1) &= \sqrt[3]{-1} \\ &= -1 \end{align*} | |
| 3. | Determine the domain of each function: |
| a) $f(x)=3x-7$ | |
| Solution: $f$ is a linear function; therefore it has no restrictions on its domain. (i.e. domain $\; = \; x\in\mathbb{R}$) |
|
| b) $f(x)=\sqrt[6]{5-2x}$ | |
| Solution. $f$ is an $n$th-root function, where $n=6$ is even. Therefore, it's only defined when the expression under the radical is greater than or equal to zero. i.e. we must sove the inequality: $5-2x \geq 0.$ \begin{align*} 5-2x \geq 0 &\Rightarrow 5 \geq 2x \\ & x \leq \frac{5}{2} \end{align*} Therefore, domain $ \; = \; \left\{x \in \mathbb{R} \; \large| \; x \leq \frac{5}{2}\right\}$ | |
| c) $f(x)=\frac{\sqrt{x-4}}{x^2-6x+5}$ | |
| Solution. $f$ is a quotient of two functions, $\frac{g(x)}{h(x)}.$ Thus we can write $f$ as a product of two functions, $f(x)= g(x) \cdot \frac{1}{h(x)}.$ The domain of a product of two functions must satisfy the restrictions of the two. In other words,
$$domain(f(x)) = domain(g(x))\cap domain\left(\frac{1}{h(x)}\right)$$ Here, $g(x) = \sqrt{x-4}$ and $ h(x)=x^2-6x+5$. So, $domain\left(g(x)\right)$ includes all real number $x$ such that $x-4\geq 0$. $$\Rightarrow domain\left(g(x)\right) = \left\{x \in \mathbb{R} \; \large| \; x \geq 4 \right\} \qquad (*) .$$ Furthermore, because $h(x)$ is in the denominator, $domain\left(\frac{1}{h(x)}\right)$ includes all real numbers $x$ such that $h(x) \neq 0$. i.e. we require that $$x^2-6x+5 = (x-5)(x-1) \neq 0.$$ So $x \neq 5$ and $x \neq 1$. This gives: $$domain\left(\frac{1}{h(x)}\right) = \left\{x \in \mathbb{R} \; \large| \; x \neq 5 \textrm{ and } x \neq 1 \right\} \qquad (**) .$$ Finally, taking the intersection of $(*)$ and $(**)$, we have: $$domain(f(x)) = \left\{x \in \mathbb{R} \; \large| \; x \geq 4 \textrm{ and } x \neq 5 \right\} .$$ |
