Mathematical Statements
Worked Examples
Mathematical Statements
Brielfy a mathematical statement is a sentence which is either true or false. It may contain words and symbols. For example ``The square root of 4 is 5" is a mathematical statement (which is, of course, false). In mathematics we use language in a very precise way, and sometimes it is slightly different from every day use. We will begin by discussing some differences which often arise.Part 1. "Either/Or"
In every day language we use the phrase "either A or B" to mean that one of the two options holds, but not both. For example, when most people say something like ``You can have either a hot dog or hamburger," they usually aren't offering you both. The use of ``either/or" in everyday English is usually divisive, and meant to imply there are only two options: A or B, but not both A and B. (The use of "or" in this way is sometimes referred to as "exclusive or.")However, the use of "either A or B" in mathematics allows the option that both A and B hold. (The use of "or" in this way is sometimes referred to as "inclusive or.")
For example, in mathematics, the statement "If $x$ is a real number, then either $x\leq 0$ or $x\geq 0$" allows the possibility that $x$ satisfies both $x\leq 0$, as well as $x\geq 0$ (which is true of the real number $0$). If we think about this statement we can see that it is true, since any real number satisfies at least one of these inequalities. However, if we took the common use of "either/or" we would think that this statement is false, since it is possible to satisfy both inequalities.
Part 2. "And"
In mathematics the use of "and" also deserves a brief discussion, although its use agrees with the everyday use. Just as we would expect, the phrase "A and B" means that both A and B must hold. For example, consider the statement "If $n$ is an integer that is divisible by 4, then $\frac{n}{2}$ and $\frac{n}{4}$ are integers." For an integer to be divisible by 4, it must be true that $\frac{n}{2}$ is an integer and $\frac{n}{4}$ is an integer.One can make use of Venn Diagrams to understand the use of ``either/or" as well as ``and" as illustrated in the diagram below.
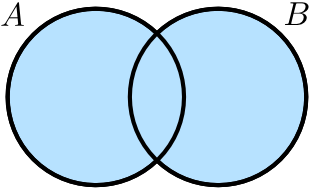 |
 |
|
"either A or B" |
"A and B" |
