Finite-time Blow-up of Solutions of Some Long-wave Unstable Thin Film Equations
with A. L. Bertozzi,
Indiana Univ. Math. J. 49(2000)4:1323-1366.
to appear in Indiana University Mathematics Journal
Abstract
We consider the family of long-wave unstable lubrication equations
ht = -(h hxxx)x - (hm hx)x
with 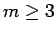 .
Given a fixed
.
Given a fixed 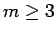 ,
we prove the existence of a
weak solution that becomes singular in finite time. Specifically,
given compactly supported nonnegative initial data with negative
energy, there is a time
,
we prove the existence of a
weak solution that becomes singular in finite time. Specifically,
given compactly supported nonnegative initial data with negative
energy, there is a time
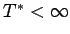 ,
determined by m and the
H1 norm of the initial data, and a compactly supported nonnegative
weak solution such that
,
determined by m and the
H1 norm of the initial data, and a compactly supported nonnegative
weak solution such that
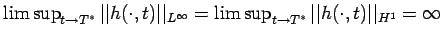 .
We discuss the relevance of these singular solutions to an earlier
conjecture [Comm Pure Appl Math 51:625-661, 1998] on when
finite-time singularities are possible for long-wave unstable
lubrication equations.
.
We discuss the relevance of these singular solutions to an earlier
conjecture [Comm Pure Appl Math 51:625-661, 1998] on when
finite-time singularities are possible for long-wave unstable
lubrication equations.
click here for the *.ps file of
the article.
click here for the *.pdf file of
the article.
We thank Andrew J. Bernoff for pointing out the formal second moment
argument upon which the finite-time blow-up proof hinges. M. P. thanks
Richard S. Laugesen for useful mathematical conversations.
A. B. was supported by an ONR Young Investigator/PECASE award and an
Alfred P. Sloan Research Fellowship. M. P. was supported by NSF grant
number DMS-9971392 and an Alfred P. Sloan Research Fellowship.