
May 1997 Presentation Topic (continued)



May 1997 Presentation Topic (continued)
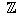 on a blackboard
where bold-face is unavailable); this is because 19th century mathematics
was dominated by German mathematicians and the integers are called
Zahlen in German).
on a blackboard
where bold-face is unavailable); this is because 19th century mathematics
was dominated by German mathematicians and the integers are called
Zahlen in German).
The algebraic structure of the integers is very rich and is the subject of Number Theory. Questions about the distribution of prime numbers are among the most difficult open problems in mathematics. One amazing result is that, for large numbers N, the number of primes from 1 to N is on the order of N / log(N); this fact (which can be stated more precisely) is known as the Prime Number Theorem.
The integers are adequate for describing whole quantities but not portions of quantities. For this purpose, a new concept must be defined: that of a rational number. A rational number can be defined to be a pair of integers r and s (with s non-zero), representing r pieces, where s pieces make up a whole. We write this pair of numbers using the notation r/s, and we consider two pairs r/s and m/n to be the same rational number if nr - ms = 0.
(Mathematical sophisticates would say that the rational numbers are equivalence classes of pairs (r,s) under the equivalence relation that relates (r,s) to (m,n) if and only if nr - ms = 0, and that the equivalence class of the pair (r,s) is denoted r/s).
Since not all lengths are expressible within it, the rational number system, although adequate for counting possessions, recording transactions, and counting portions of things, is inadequate for measuring lengths. A new kind of number must be constructed for that purpose. The square root of 2 is an example of this new kind of number: it measures the length of the diagonal of a square of side length 1, but it is not one of the familiar rational numbers so beloved by the Greeks.
Real numbers need to be able to describe lengths and other continuous quantities, even ones not representable by rational numbers (like the diagonal of a unit square). In short, they need to be able to describe all possible locations on the "number line". How can we construct such numbers out of rational numbers (the only kind that we so far know to exist)?
There are two ways. One is to describe a location on the number line by saying which rational numbers lie below it and which lie above it. A real number can then be defined as a partition of the rationals into two groups, satisfying certain properties (like the fact that everything in group 1 must be less than everything in group 2).
Another way (a little less elegant but more useful for writing down real numbers) is to describe a location on the number line by a sequence of rational numbers which form better and better approximations to it. One can then define a real number to be any such sequence of rational numbers.
Not all sequences converge
to a single location on the number line, so we consider
only Cauchy sequences. These are sequences
such that, for any positive number 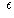 (no matter how small),
there is some place in the
sequence such that, from that point on, all terms are within
(no matter how small),
there is some place in the
sequence such that, from that point on, all terms are within 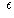 of
each other. This guarantees that the sequence is forming better and
better approximations to a single location on the number line.
of
each other. This guarantees that the sequence is forming better and
better approximations to a single location on the number line.
Two sequences 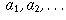 and
and 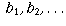 may
define the same location on the number line. This happens if the
differences
may
define the same location on the number line. This happens if the
differences 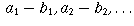 are converging
to zero (meaning that, for any positive number
are converging
to zero (meaning that, for any positive number 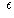 , all the differences
from some point on are smaller than
, all the differences
from some point on are smaller than 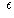 in absolute value).
In this case, we call the sequences "equivalent".
in absolute value).
In this case, we call the sequences "equivalent".
Now we define a real number to be an equivalence class of Cauchy sequences of rational numbers (that is, each Cauchy sequence defines a real number, and two Cauchy sequences define the same real number if and only if they are equivalent). This should remind you of the way rational numbers were defined as pairs of integers, with two pairs (r,s) and (m,n) defining the same rational number if and only if nr - ms = 0.
We can write real numbers in decimal notation, for example,
pi = 3.1415. . . . What this means is we are looking at the
real number defined by the following sequence of rational numbers:
3, 3.1, 3.14, 3.141, 3.1415, . . . (this is a Cauchy sequence
because, for any n, after the nth term all terms agree to n decimal
places and hence are within 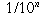 of each other). Any decimal
expression defines a Cauchy sequence of rational numbers (by truncating
at successive decimal places), and hence every decimal expression
defines a real number.
of each other). Any decimal
expression defines a Cauchy sequence of rational numbers (by truncating
at successive decimal places), and hence every decimal expression
defines a real number.
Another interesting property is that there are the same number of rational numbers as there are integers (even though the rational numbers contain all the integers and more besides!), but there are more real numbers than there are integers.
The well-ordering constructed in the solution to question 4 provides a
way to put the positive rational numbers into 1-1 correspondence with
the positive integers (which is what it means to say that there are
as many positive rational numbers as positive integers): for every
positive rational number r, there are only finitely many other
numbers s for which 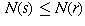 , so there are only
finitely many numbers s which are smaller than r under the
new ordering. This means that if you start with the smallest positive rational
number, label it "1", label the next smallest "2", and so on,
you will eventually reach every postive rational number r. In this
way, every positive rational number r gets matched with a positive
integer, leaving nothing out.
, so there are only
finitely many numbers s which are smaller than r under the
new ordering. This means that if you start with the smallest positive rational
number, label it "1", label the next smallest "2", and so on,
you will eventually reach every postive rational number r. In this
way, every positive rational number r gets matched with a positive
integer, leaving nothing out.
However, the real numbers can not be put into 1-1 correspondence with the integers. There's a famous argument called Cantor's diagonalization argument which proves this; we will not go any further into this here.
Note that this is the same sort of thing as a congruence
statement on the integers: when "4", "5", and "2" stand for integers
instead of clock-face hours, then
it is no longer true that 4+5=2, but what is
true is that 4+5=9 and 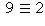 (mod 7).
(mod 7).
Rather than work with integers and congruence relations modulo 7,
it is
often easier to work with a new number system (called a finite field)
which has only seven numbers: 0, 1, 2, 3, 4, 5, and 6. These can be added
or multiplied together, with the result always being in the same number
system; for instance, 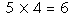 in this number system.
in this number system.
We have seen in the questions that division is well-defined in this number system, and the cancellation law holds. This is why the procedure used in solving question 7 is guaranteed to work (as long as we are working modulo a prime number).
In arithmetic modulo non-primes, the cancellation law no longer holds. For
example, in arithmetic modulo 12, 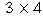 is the product of two
non-zero numbers which gives you zero. In such number systems, you cannot
divide by all
non-zero numbers. However, the structure of these number systems
is still rich with important theoretical properties.
is the product of two
non-zero numbers which gives you zero. In such number systems, you cannot
divide by all
non-zero numbers. However, the structure of these number systems
is still rich with important theoretical properties.
The definition of real numbers by Cauchy sequences relied on a notion of what the "distance" between two rational numbers r and s is. Normally, this distance is defined to be d(r,s) = |r-s|, and it is to this notion of distance we are referring when we say things like "the terms must be within eps of each other". However, there are other notions of distance which satisfy all the properties a distance function needs to satisfy. These other notions of distance have a more algebraic flavour and are very important in number theory.
For instance, consider the prime number 3. For each integer n,
define the weight W(n) of n to be the number of times 3
divides n. For each rational number m/n, define its weight
W(m/n) to be W(m)-W(n). Now define the distance between two
rational numbers r and s to be  .
.
Notice that two integers are very close together if their difference is divisible by a high power of 3. This is a pretty weird distance function, but it satisfies all the properties a distance function has to satisfy, so we can define the notion of Cauchy sequences of rational numbers with respect to this distance function. This collection of Cauchy sequences forms a number system called the 3-adic numbers, in the same way that the usual Cauchy sequences of rational numbers form the real number system.
In the same way, one can define "p-adic numbers" for any prime p.
Other interesting number systems include the algebraic numbers, that
is, numbers which can be described as roots of polynomial equations with
rational coefficients. An example of an algebraic number is  ,
a root of the equation
,
a root of the equation 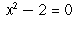 .
For a while people wondered whether all real numbers might be
algebraic, but the answer is no. In fact, there are many more
non-algebraic real numbers
than there are algebraic ones: the algebraic numbers can be put into 1-1
correspondence with the integers, but the real numbers cannot.
.
For a while people wondered whether all real numbers might be
algebraic, but the answer is no. In fact, there are many more
non-algebraic real numbers
than there are algebraic ones: the algebraic numbers can be put into 1-1
correspondence with the integers, but the real numbers cannot.
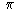 and e are examples of non-algebraic real numbers.
and e are examples of non-algebraic real numbers.
Finally, there are the complex numbers. These can be defined as pairs of real numbers (a,b), typically written in the notation a + bi. With the appropriate definition of addition and multiplication, the pair 0+1i (usually written just as "i") squares to give -1. The fundamental importance of the complex numbers is given by
The Fundamental Theorem of Algebra. Every polynomial with coefficients in the complex numbers has a root that is a complex number.This is not true for the real numbers (for example, the equation
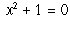 has no real-valued roots), and it is what makes the complex
numbers so useful, especially when trying to talk about geometry in
algebraic terms.
has no real-valued roots), and it is what makes the complex
numbers so useful, especially when trying to talk about geometry in
algebraic terms.


![]() Go backward to Solutions
Go backward to Solutions![]() Go up to Introduction and Contents
Go up to Introduction and Contents![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer) Go to SIMMER Home Page
Go to SIMMER Home Page Go to The Fields Institute Home Page
Go to The Fields Institute Home Page![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page