
Society Investigating Mathematical Mind-Expanding Recreations



Society Investigating Mathematical Mind-Expanding Recreations
This is a summary of what was presented and discussed at the February 26th SIMMER meeting, along with some problems and questions to think about.
We start from the basic idea of a set, or collection of objects.
For example, the set of all prime numbers, or the set of inhabitants of
Ontario in January 1998. Two sets are the same if
they have exactly the same members;
for example, the set of all even prime numbers greater than 2
is the same set as the set of all unicorns, namely the empty set
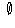 with no members. A set A is a subset of
a set B if every member of A is a member of B;
A is a proper subset of B if it is a subset of B, but
B is not a subset of A.
For example, the set of all prime numbers is a proper subset of
the set of all integers.
with no members. A set A is a subset of
a set B if every member of A is a member of B;
A is a proper subset of B if it is a subset of B, but
B is not a subset of A.
For example, the set of all prime numbers is a proper subset of
the set of all integers.
Cantor defined two sets to have the same cardinal number if
they can be put in one-to-one correspondence with each other.
We write |X| for the cardinal number of a set X;
for example, if X is the set {1,2,3}, then
|X| = 3.
By this definition, the set of positive even integers and the set of
all positive integers have the same cardinal number, because we can set up
the one-to-one correspondence
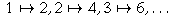 .
This may seem surprising since there are infinitely many odd positive
integers, so it seems there should be more positive integers
than even positive integers.
But remember we are talking about an infinite set.
In fact, we can take it as a definition of an infinite set
that there is a one-to-one correspondence between the set and
a proper subset of itself.
So, according to our definition, all we have proved is that the positive
integers form an infinite set, which is as it should be.
.
This may seem surprising since there are infinitely many odd positive
integers, so it seems there should be more positive integers
than even positive integers.
But remember we are talking about an infinite set.
In fact, we can take it as a definition of an infinite set
that there is a one-to-one correspondence between the set and
a proper subset of itself.
So, according to our definition, all we have proved is that the positive
integers form an infinite set, which is as it should be.
Problem 1: Let (0,1) stand for the open unit interval, that is to say, the set of points on a line strictly between 0 and 1; for example, 0.5 and 0.99999999 belong to the set (0,1), but 0 and 1 don't. Show that there is a one-to-one correspondence between the open unit interval (0,1) and the set of all real numbers, that is to say, the set of all points on an infinite straight line. (Hint: It may help to think in terms of geometrical pictures here.)
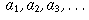 .
The cardinal number of a denumerable set was written by Cantor
as
.
The cardinal number of a denumerable set was written by Cantor
as 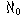 , pronounced "aleph nought" or "aleph zero."
, pronounced "aleph nought" or "aleph zero."
Problem 2: A positive rational number can be written as a fraction a/b; notice that two different fractions can represent the same rational number, for example, 2/3 = 4/6. Show that the set of all positive rational numbers is denumerable. (Hint: Think of a way of listing all fractions systematically, and then eliminating repetitions.)
Here is a slightly trickier problem along the same lines. Let's define a word to consist of a finite string of lower case letters from the English alphabet. For example, `aaa', `abcazfajdksl' and `fehfiskebvkdowjkmd' are all words according to this definition.
Problem 3: Show that the set of all words is denumerable.
A real number is defined to be algebraic if it is the root of an equation
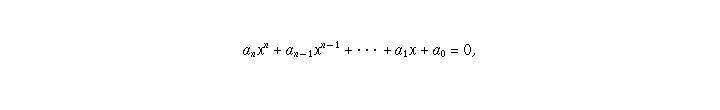
where 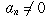 , and all the
, and all the 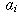 's are integers.
For example, although
's are integers.
For example, although 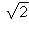 is not a rational number, it
is an algebraic number, since it is a root of the equation
is not a rational number, it
is an algebraic number, since it is a root of the equation
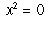 .
The next problem should not be too hard, if you have figured out
how to do the last one.
.
The next problem should not be too hard, if you have figured out
how to do the last one.
Problem 4: Show that the set of all algebraic numbers is denumerable.
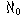 is the
only infinite cardinal number.
It was perhaps Cantor's greatest discovery that this is not so.
is the
only infinite cardinal number.
It was perhaps Cantor's greatest discovery that this is not so.
Problem 5:
Show that the set of all sets of positive integers is not
denumerable.
(Hint: Assume that you can list all sets of positive integers
as 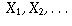 , and then, to get a contradiction, try to
define a set that is not in the list.
This is not an easy problem if you haven't seen it before!)
, and then, to get a contradiction, try to
define a set that is not in the list.
This is not an easy problem if you haven't seen it before!)
We can generalize the result of the last problem.
For any set X, we define the powerset of X,
written 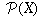 , to be the set of all subsets of X, including
the empty set. If X is a finite set with 5 members, for
example, then
, to be the set of all subsets of X, including
the empty set. If X is a finite set with 5 members, for
example, then 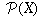 has
has 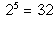 members.
If X and Y are two sets, and there is a one-to-one
correspondence between X and a subset of Y, then
we say that the cardinal number of X is less than equal to that
of Y, written
members.
If X and Y are two sets, and there is a one-to-one
correspondence between X and a subset of Y, then
we say that the cardinal number of X is less than equal to that
of Y, written 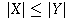 .
If
.
If 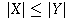 , but
, but 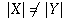 , then we say that
|X| is strictly less than |Y|, written |X| < |Y|.
, then we say that
|X| is strictly less than |Y|, written |X| < |Y|.
Problem 6:
For any set X, show that the cardinal number of X is strictly
less than the cardinal number of 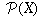 , i.e.,
, i.e.,
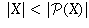 .
.
So, from the result of problem 6, we know that not only is there more than one infinite number, there is actually an infinite ascending sequence of them. Cantor's hierarchy of infinite numbers starts

and on into the mists of the transfinite where only hardened professional set theorists dare to peep!
Here is one more problem about comparing sizes of infinite numbers. It is not quite as easy as it looks.
Problem 7: Let X be an infinite set (defining "infinite" as we did above). Show that X has a denumerable subset.
The answer to the last problem shows that 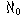 is
the smallest infinite number.
The answer to the problem involves a famous axiom of
set theory known as "the axiom of choice," since it allows
us to define a set by performing infinitely acts of
selection or "choice."
is
the smallest infinite number.
The answer to the problem involves a famous axiom of
set theory known as "the axiom of choice," since it allows
us to define a set by performing infinitely acts of
selection or "choice."
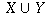 , that is, the set whose members are all
the members of X together with all the members of Y.
In symbols,
, that is, the set whose members are all
the members of X together with all the members of Y.
In symbols, 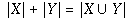 .
.
Problem 8: Show that 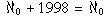 and
that
and
that 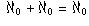 .
.
To multiply two infinite numbers, we proceed as follows.
Let X and Y be two sets with cardinal numbers |X| and
|Y|. Then the product of |X| and |Y|, which we'll write
as 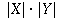 , is the cardinal
number of the Cartesian product
, is the cardinal
number of the Cartesian product 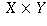 of X and Y, that is to
say, the set of all ordered pairs
of X and Y, that is to
say, the set of all ordered pairs 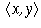 ,
where x is in X and y is in Y.
,
where x is in X and y is in Y.
Problem 9:
Show that 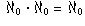 .
.
Problem 10:
Let C be the cardinal of the continuum, that is,
the cardinal of the set of all positive real numbers less than or equal
to 1.
Show that 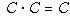 .
.
The answer to Problem 10 is intuitively surprising, because it can be interpreted as saying that there exactly as many points on a line as in a two-dimensional space, thus showing that the notion of dimension cannot be characterized in terms of cardinality. This seemed so surprising to Cantor that when he discovered it in 1878 he wrote in a letter to his friend Richard Dedekind: "I see it, but I don't believe it!"
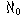 is the cardinal number
of the set N of positive integers.
The answer to Problem 5 shows that the cardinal number
is the cardinal number
of the set N of positive integers.
The answer to Problem 5 shows that the cardinal number
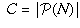 is strictly greater than
is strictly greater than 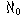 .
This number is also known as the number of the continuum,
because it is the number of all points in the continuum of
three-dimensional space.
.
This number is also known as the number of the continuum,
because it is the number of all points in the continuum of
three-dimensional space.
Problem 11: Is there a cardinal number strictly
between 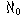 and the number C of the continuum?
and the number C of the continuum?
Problem 11 is known as Cantor's Continuum Problem. It is still unsolved, but we also know that in a certain sense it is unsolvable. It has been proved that the problem cannot be solved using only the commonly accepted assumptions of the modern theory of sets. Whether the problem can be solved by inventing new axioms about sets and numbers is a difficult problem in the philosophy of mathematics.


![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer) Go to SIMMER Home Page
Go to SIMMER Home Page Go to The Fields Institute Home Page
Go to The Fields Institute Home Page![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page