
Society Investigating Mathematical Mind-Expanding Recreations



Society Investigating Mathematical Mind-Expanding Recreations
| Trial by Jury | Statistical Hypothesis Testing |
| Prosecutor | Statistician |
| Trial | Collection of Data |
| Jury decides on the verdict | Statistical test |
| Assume defendant is innocent | Assume the null hypothesis is true |
| Weigh the evidence provided by | Assess the evidence provided by |
| testimony and exhibits | the data (as summarized in the test statistic) |
| assuming defendant is innocent | assuming null hypothesis is true |
| Evidence against the defendant | Calculate a p-value for the test statistic |
| assuming defendant is innocent | assuming null hypothesis is true |
| Defendant found guilty | Reject the null hypothesis if |
| beyond a reasonable doubt | p-value less than the significance level |
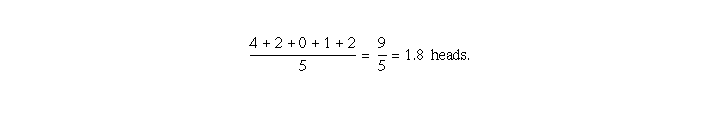
The Law of Large Numbers states that as the sample size (number of
observations) increases, the sample mean will approach the actual mean.
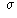 and mean
and mean 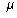 ,
we say that the data has
a Normal Distribution if 95% of the observations are within 2 standard
deviations of the mean, and 68% of the observations are within one standard
deviation of the mean, and the mean is also the median.
,
we say that the data has
a Normal Distribution if 95% of the observations are within 2 standard
deviations of the mean, and 68% of the observations are within one standard
deviation of the mean, and the mean is also the median. 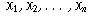 from a common
distribution, for the sample mean
from a common
distribution, for the sample mean
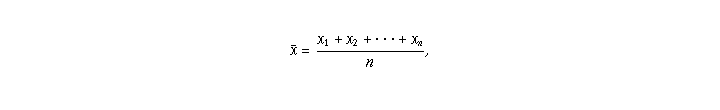
the Central Limit Theorem states that as the sample size increases, the
distribution of 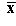 becomes closer to a normal distribution. Also, the distribution
of the sum of the random observations,
becomes closer to a normal distribution. Also, the distribution
of the sum of the random observations,
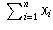 becomes closer to
a normal distribution.
becomes closer to
a normal distribution.
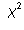 Test of Independence
Test of Independence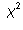 distribution
with one degree of freedom. The sum of the squares of k standard
normal random variables has a
distribution
with one degree of freedom. The sum of the squares of k standard
normal random variables has a 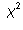 distribution with k
degrees of freedom. The number of degrees of freedom is a parameter of the
distribution. The higher the degrees of freedom, the flatter the
distribution.
distribution with k
degrees of freedom. The number of degrees of freedom is a parameter of the
distribution. The higher the degrees of freedom, the flatter the
distribution.
| Preferred Newspaper | |||
| Gender | Globe and Mail | Toronto Star | Toronto Sun |
| Male | 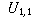 | 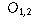 | 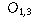 |
| Female | 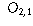 | 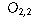 | 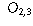 |
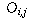 is the observed count that falls into category (i,j).
Let n be the total number of people polled (so
is the observed count that falls into category (i,j).
Let n be the total number of people polled (so 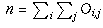 ).
Assume that there is no relationship between gender and newspaper
preference. Then applying our fact from probability theory, the probability
of a male preferring the Globe and Mail is the proportion of males times
the proportion of Globe readers; the expected number of male Globe readers
is n times that.
Call this expected count in category (i,j):
).
Assume that there is no relationship between gender and newspaper
preference. Then applying our fact from probability theory, the probability
of a male preferring the Globe and Mail is the proportion of males times
the proportion of Globe readers; the expected number of male Globe readers
is n times that.
Call this expected count in category (i,j): 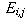 .
.
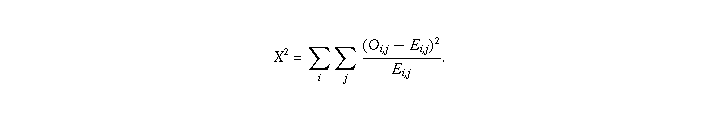
If gender and newspaper are truly independent, 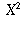 has a
has a 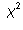 distribution on
distribution on
rc-1-(r-1)-(c-1)=(r-1)(c-1)degrees of freedom, where r is the number of rows in our table and c is the number of columns.
Note 1: We lose a degree of freedom each time we treat something as fixed, for example, the total number of males, the total number of Sun readers, etc.
Note 2: The distribution of X^2 follows from the above distribution theory, plus some calculation. See, for example, Mathematical Statistics with Applications, by Mendenhall, Wackerly, and Scheaffer.
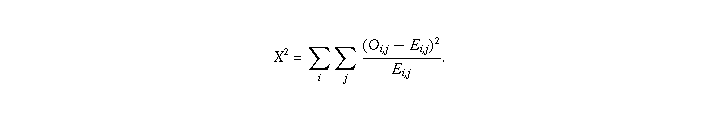
The distribution of the test statistic assuming the null hypothesis
is true: 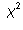 with (r-1)(c-1) degrees of freedom.
with (r-1)(c-1) degrees of freedom.
The conclusion: If the probability of getting
an 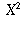 that is as large or larger
than what we got is small, we have evidence that our null
hypothesis is false.
that is as large or larger
than what we got is small, we have evidence that our null
hypothesis is false.
www.dartmouth.edu/~chance/
www.math.montana.edu/mathed/simms/
| Newspaper | |||
| Gender | Globe | Star | Sun |
| Male | |||
| Female | |||
| Words | Sense and Sensibility | Emma | Sanditon I | Sandition II |
| a PB such | 14 | 16 | 8 | 2 |
| a NPB such | 133 | 180 | 93 | 81 |
| and FB I | 12 | 14 | 12 | 1 |
| and NFP I | 241 | 285 | 139 | 153 |
| the PB on | 11 | 6 | 8 | 17 |
| the NPB on | 259 | 265 | 221 | 204 |
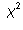 test!)
test!)
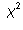 test of independence
on the following table:
test of independence
on the following table:
| Hit | No hit | |
| Regular season | 2584 | 7280 |
| World Series | 35 | 63 |
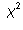 distribution
with 1 degree of freedom under the hypothesis of no relationship.
The p-value is 0.033. Whether or not the null hypothesis should
be rejected depends on the significance level. Assuming there's
no relationship between Jackson's batting average and whether or
not it's a World Series game, observing a difference as greater
or greater than what Jackson accomplished would happen 3% of
the time. Do you consider that highly unusual?
distribution
with 1 degree of freedom under the hypothesis of no relationship.
The p-value is 0.033. Whether or not the null hypothesis should
be rejected depends on the significance level. Assuming there's
no relationship between Jackson's batting average and whether or
not it's a World Series game, observing a difference as greater
or greater than what Jackson accomplished would happen 3% of
the time. Do you consider that highly unusual?
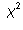 distribution with 10
degrees of freedom and a p-value of 0.0097. So it
appears that Austen was not consistent in the use of
these word combinations! So does it matter what the
imitator did?
distribution with 10
degrees of freedom and a p-value of 0.0097. So it
appears that Austen was not consistent in the use of
these word combinations! So does it matter what the
imitator did?


![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer) Go to SIMMER Home Page
Go to SIMMER Home Page Go to The Fields Institute Home Page
Go to The Fields Institute Home Page![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page