Question Corner and Discussion Area
Question Corner and Discussion Area
I have a math question that you may or may not be able to answer. If you can't answer it please refer me to someone who you believe can. I am in calc2 so your answer can be somewhat complex.The number this sequence converges to is the unique solution to the equation x = cos x. In other words, it is the place where the graph of the function f(x) = x - cos x crosses the x-axis. Let's call this number z.My question is:
I have fallen upon the sequence a(n) = cos(a(n-1)).
My question is, what does this sequence converge on? I know that it goes towards a number that is about 0.73. . . . In fact I can find the value to about 12 decimal places using a calculator but I am interested in finding out what this number is (in terms of other things like integers,
, e, or other things).
I understand if you don't have time to answer but please reply.
Thank you for your time,
John Koehler
First, let me explain how we know such a number z exists, and why it is unique.
Its existence follows from the intermediate value theorem:
f(0) = 0-1 < 0 while 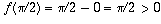 , and
f is a continuous function, so there must be some number z in
between 0 and
, and
f is a continuous function, so there must be some number z in
between 0 and 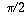 with the property that f(z)=0.
with the property that f(z)=0.
The reason this number z is unique is that the function f is
non-decreasing: its derivative is 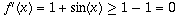 .
In order for it to have two roots, it would have to either be
constant between them (which it clearly is not; there is no interval
on which x - cos(x) stays constant), or else it would have
to be decreasing somewhere (if it increases after passing through
the first root, it would have to decrease again to get back to zero),
and this can't happen because f is non-decreasing.
.
In order for it to have two roots, it would have to either be
constant between them (which it clearly is not; there is no interval
on which x - cos(x) stays constant), or else it would have
to be decreasing somewhere (if it increases after passing through
the first root, it would have to decrease again to get back to zero),
and this can't happen because f is non-decreasing.
This explains how the number z is uniquely defined by the equation cos(z)=z.
The reason the sequence converges to this number z is as follows. Let's look at how close a(n) is to this number z: the absolute value of the difference is |a(n)-z| = |cos(a(n-1))-z|. Since z=cos(z), this is the same as |cos(a(n-1))-cos(z)|.
By the mean value theorem, any expression of the form g(b)-g(a) equals g'(t)(b-a) for some number t in between a and b (assuming g is differentiable on the interval [a,b]). I hope you have seen this theorem in your calculus class; if not, let us know and we can explain further.
Therefore, |a(n)-z| = |cos(a(n-1))-cos(z)| = |sin(t)| |a(n-1)-z|.
Now, regardless of what the first term of the sequence is, the second and all subsequent terms are the cosine of something and hence are between -1 and 1. So too is the number z, so the number t above will also be between -1 and 1. On this interval the sine function is strictly increasing, so |sin(t)| < |sin(1)|.
Applying this inequality to the above expression, we get
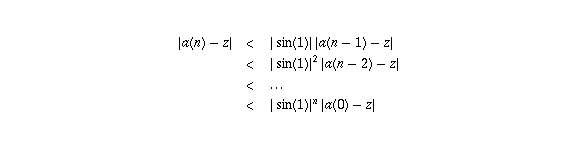
Since |sin(1)| < 1, this goes to zero as 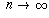 ,
proving that the sequence converges to z.
,
proving that the sequence converges to z.
This is all a special case of a general theorem called the contraction mapping principle. Any time you have a function F. an interval [a,b], and a number e < 1, with the property that (a) F(x) is in the interval whenever x is, and (b) |F(x)-F(y)| < e|x-y| for all x and y in the interval, then there is guaranteed to be a unique number z (called a fixed point) in [a,b] for which F(z)=z, and, if you start with any number x in [a,b] and look at the sequence x, F(x), F(F(x)), . . . , it converges to z.
Now, finally, for the main point of your question: is there any simpler
way to express the number z (as a combination of familiar numbers,
like integers, e, and 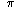 ), other than simply calling it "the
solution to the equation cos(z)=z"?
), other than simply calling it "the
solution to the equation cos(z)=z"?
The answer is no. This number z cannot be expressed any more simply, in terms of "familiar" numbers. This is true for the roots of almost any transcendental equation; for more information, see the answers to other questions on this topic.
If you were in a context where you needed to work with this number a lot,
you'd simply give it a name, in much the same way as people gave names
to the numbers 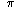 and e.
and e.
![]() Go backward to Solution to the Transcendental Equation 2^x + 3^x = 5
Go backward to Solution to the Transcendental Equation 2^x + 3^x = 5![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Solving a Quadratic with Non-Constant Coefficients
Go forward to Solving a Quadratic with Non-Constant Coefficients![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page