Question Corner and Discussion Area
Question Corner and Discussion Area
What is the use of scientific notation in every day life?Scientific notation is needed any time you need to express a number that is very big or very small. Suppose for example you wanted to figure out how many drops of water were in a river 12 km long, 270 m wide, and 38 m deep (assuming one drop is one millilitre). It's much more compact and meaningful to write the answer as roughly
 than it is to
write 123120000000000.
than it is to
write 123120000000000.
For one thing, the scientific notation is easier to read, and makes it much easier to tell at a glance what the order of magnitude is (rather than counting zeros).
For another, most of the digits in 123120000000000 are completely meaningless (unless your measurements were very precise). For instance, if the exact river length were really 12.123123 km (we just measured it to the nearest kilometre), then correct number of drops would be 124383242000000, and after the first three digits our result of 123120000000000 is quite inaccurate. So it's better to use a notation (like scientific notation) in which you can suppress the inaccurate digits.
Who created scientific notation? What are the uses for it in the work field?Scientific notation was not "created", in the sense of someone coming up with something new. The fact that
 happens to
equal 30000 is a mathematical truth, not a creation.
happens to
equal 30000 is a mathematical truth, not a creation.
The question becomes, though, when did it become commonplace to write the first form instead of the second form. (It would be sort of like people starting to write 2+3 whenever they meant 5; that's not creating something new, merely saying something in a different way).
I do not know who first used scientific notation. The concept would be
very old; you'd have to
dig back to the first time someone thought of
describing 10000000000 as "a one followed by ten zeros", realized
that's the same as 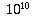 , and wrote it that way (in whatever
notation they were used to using for exponents).
, and wrote it that way (in whatever
notation they were used to using for exponents).
The modern notation for exponents (writing them raised at a higher
level) originated with Descartes
in 1637, so you would never have seen an expression like
 before then. Sometime between then and the present
it became common to write large and small numbers that way, as well
as numbers where it's important to convey an indication of the
precision of a measurement; I do not
know when it became common practice or who started doing it, but I
will see if I can find out. It most likely occurred during the 1800's and
1900's when scientists were developing their understanding of the
astronomical universe (involving really huge numbers to describe distances), and
of the world of subatomic particules (involving really small numbers).
before then. Sometime between then and the present
it became common to write large and small numbers that way, as well
as numbers where it's important to convey an indication of the
precision of a measurement; I do not
know when it became common practice or who started doing it, but I
will see if I can find out. It most likely occurred during the 1800's and
1900's when scientists were developing their understanding of the
astronomical universe (involving really huge numbers to describe distances), and
of the world of subatomic particules (involving really small numbers).
I don't know that I can say in answer to the question "what are the uses for it in the work field", other than what I've already said in answer to the previous question on this page: it would be needed any time you are dealing with numbers that are very large or very small, and any time you make a measurement of something and want to write the number in a way that gives an indication of its precision.
For example, if you're an engineer and you want to record the pressure
on a supporting beam of a bridge, and you measure it as 500034 but your
instrument is only precise to 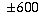 , you would not want to
write "500034" because you really have no way of knowing, based on
your measurement, what the last few digits are. On the other hand, you
wouldn't want to just round it to 500000, because that doesn't convey
the fact that you do precisely know the first few digits!
Scientific notation (
, you would not want to
write "500034" because you really have no way of knowing, based on
your measurement, what the last few digits are. On the other hand, you
wouldn't want to just round it to 500000, because that doesn't convey
the fact that you do precisely know the first few digits!
Scientific notation (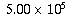 ) is the perfect way to express
the number and give an idea of how precise it is.
) is the perfect way to express
the number and give an idea of how precise it is.
So, the answer to your question is, just pick any field in which people deal with large and small numbers, and/or make measurements of quantities and need to write them in a way that indicates how precise the measurements are.
![]() Go backward to Applications of the Geometric Mean
Go backward to Applications of the Geometric Mean![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Natural Logs in the Real World
Go forward to Natural Logs in the Real World![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page