Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE) (These buttons explained below)
UNIVERSITY OF TORONTO MATHEMATICS NETWORK

Question Corner and Discussion Area

Four-dimensional Pyramids

Asked by Anders Ericson, student, Sweden on November 12, 1997:
Hi,

My name is Anders Ericson and I am a Swedish Student on my 12th year (is that equal to college)

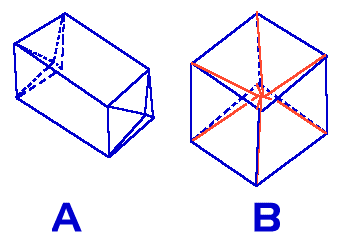
I program a lot and have made a program that draws a 4D cube as well as a 5- and 6D cube. Now I'm wondering how a 4D pyramid looks like (an egyptian pyramid with a square bottom). I've come up with two alternatives that I have drawn in the attached GIF-file.

Figure A is supposed to be a stretched cube with a pyramid cut out in the bottom and placed at the top. Figure B is a normal cube with lines from all the corners in to the middle, that means that its created by six normal pyramids.

I think that it is the B figure that is right but it can also be some other figure.

Anders Ericson

Picture B would be a correct depiction of a 4-dimensional pyramid with a "square" bottom.

That is to say: if in 3 dimensions you have a pyramid consisting of a square bottom and an additional top vertex that is joined to all the vertices of this square, then the 4-dimensional analogue of this would be a figure that has a cubical bottom and an additional vertex that is joined to all the vertices of this cube. Your picture B depicts this.

The sides of this pyramid are 3-d pyramids, whose base is one of the square faces of the bottom cube. This is analgous to the fact that the sides of a 3-d pyramid are 2-d pyramids (triangles) whose base is one of the line segments of the bottom square.

I'm not entirely sure of the details of your picture A, such as what the dashed lines are meant to represent. However, it does not appear to be a correct description of the pyramid, because I cannot see any vertex with valence 8 (a vertex that has 8 edges emanating from it), which the true pyramid must have because the top vertex is adjacent to all 8 of the vertices of the bottom cube.

These square-based 3-d pyramids and cube-based 4-d pyramids are not actually the most natural mathematical objects. More natural is the 3-d tetrahedron (a pyramid whose base is a triangle rather than a square). The 4-dimensional analogoue of this is discussed in the answer to another question.

[ Submit Your Own Question ] [ Create a Discussion Topic ]
This part of the site maintained by (No Current Maintainers)
Last updated: April 19, 1999
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE)

(IMAGE) Go backward to Fractals and their History
(IMAGE) Go up to Question Corner Index
(IMAGE) Go forward to Euclidean Geometry
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Access printed version in PostScript format (requires PostScript printer)
(IMAGE) Go to University of Toronto Mathematics Network Home Page