Question Corner and Discussion Area
Question Corner and Discussion Area
Please tell me about the concepts of infinity,Before I begin, I will note that a truly detailed account of any of these topics could easily fill a book (I know that there is at least one book dedicated to the history ofand symmetry.
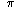 and I have little doubt that
there are entire books on symmetry as well). What follows are a few
words about each topic.
and I have little doubt that
there are entire books on symmetry as well). What follows are a few
words about each topic.
For information about infinity, refer to the page Does Infinity Exist?.
Pi is, quite simply, a number.
It has been known of since ancient times --
there are references to it in the Bible and in Greek literature,
to name a few.
Over the years we have gained more and more knowledge of 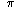 and calculated it to progressively greater and greater precisions
(it is now known to millions of decimal places).
and calculated it to progressively greater and greater precisions
(it is now known to millions of decimal places).
The definition of 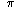 is remarkably simple.
It is the ratio between the circumference and diameter of a circle.
To a few decimal places its value is 3.14159265. . . .
Similar to the square root of 2,
it is an irrational number and its digits never repeat.
In this sense (and others) it is somewhat pathological.
is remarkably simple.
It is the ratio between the circumference and diameter of a circle.
To a few decimal places its value is 3.14159265. . . .
Similar to the square root of 2,
it is an irrational number and its digits never repeat.
In this sense (and others) it is somewhat pathological.
Nevertheless, 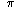 turns up frequently in applied
mathematics problems, sometimes in surprising ways.
For instance, the sum
1 + 1/4 + 1/9 + 1/16 + 1/25 +. . . converges to
turns up frequently in applied
mathematics problems, sometimes in surprising ways.
For instance, the sum
1 + 1/4 + 1/9 + 1/16 + 1/25 +. . . converges to 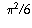 (you may see the proof of this in a calculus course some day).
(you may see the proof of this in a calculus course some day).
It turns out that there is a unit of angular measure
frequently used in mathematics which involves 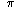 .
If two lines intersect at a point, we can measure the angle between them
as follows.
Draw a circle (with any radius you like) centered at the point where the
lines cross.
Now the measure of the angle is given by the length of its arc on the circle
divided by the radius of the circle.
This is the measure of the angle in radians.
There are
.
If two lines intersect at a point, we can measure the angle between them
as follows.
Draw a circle (with any radius you like) centered at the point where the
lines cross.
Now the measure of the angle is given by the length of its arc on the circle
divided by the radius of the circle.
This is the measure of the angle in radians.
There are 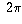 radians in a full circle and we can therefore
convert degrees to radians by multiplying by
radians in a full circle and we can therefore
convert degrees to radians by multiplying by 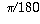 .
.
Symmetry is one of Mathematicians' greatest friends, as it often helps to simplify their lives. It is difficult to define exactly what it is, though it always refers to some sort of self-similarity of an object. This sort of repetition allows us to study a small part of an object and still have a good feel for how it behaves as a whole.
Often this symmetry is in the form of a reflection: one half of the object
is the mirror image of the other half of the object.
Consider the graph of the parabola 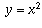 .
The section of the parabola to the right of the y-axis is
just a reflection of the other half of the parabola.
.
The section of the parabola to the right of the y-axis is
just a reflection of the other half of the parabola.
Other times symmetry occurs as reflection through a point.
The graph of the curve 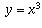 exhibits this type of symmetry.
If we wanted to find the signed area between this curve and the
x-axis between the lines x = -1 and x = +1, we could note that
the area to the left of the y-axis has the same value, with a change of
sign, as the area to the right of the y-axis. Without performing any
significant calculations we can use symmetry to deduce that the total area
is 0.
exhibits this type of symmetry.
If we wanted to find the signed area between this curve and the
x-axis between the lines x = -1 and x = +1, we could note that
the area to the left of the y-axis has the same value, with a change of
sign, as the area to the right of the y-axis. Without performing any
significant calculations we can use symmetry to deduce that the total area
is 0.
Geometric solids often exhibit some sort of useful symmetry. Suppose we wanted to calculate the volume of an icosahedron (a 20 sided object whose faces are all equilateral triangles). The task seems difficult if we fail to notice that our solid is simply 20 identical pyramids glued together. We can just find the volume of one of these pyramids and then find the volume of the whole icosahedron by multiplying by 20.
Symmetry can occur in more subtle ways as well. Sometimes proofs themselves exhibit some symmetry. Instead of repeating one's self, authors often prove only one of the cases of a theorem. They then argue that the other similar cases are proved in a symmetric way.
![]() Go backward to Why The Midpoint Formula Works
Go backward to Why The Midpoint Formula Works![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Why is e^(pi*i) = -1?
Go forward to Why is e^(pi*i) = -1?![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page