Question Corner and Discussion Area
Question Corner and Discussion Area
I put in a test the following question.Your student's answer is perfectly correct, except that there's a step missing: the discriminant of the quadratic isProve that the following equation has no roots:(I had in mind a graphical solution.).
A student gave me the following solution:
He is "sort of right" but I am "afraid" of allowing students to solve for x with respect to x. What do you think?.
has to be
to have solutions. sin x cannot be >1, so the equation has no solutions.
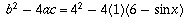 , which is 4(sin x - 2)
rather than just sin x - 2. However, the extra factor of 4 does not
affect the sign of the discriminant.
, which is 4(sin x - 2)
rather than just sin x - 2. However, the extra factor of 4 does not
affect the sign of the discriminant.
The answer is correct because, if x, a, b, and c are any
four real numbers which satisfy the relationship  (*),
then the discriminant
(*),
then the discriminant 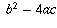 must be non-negative. If there were
a solution x to your original equation, then the four numbers
x, a=1, b=-4, and c = 6 - sin x would satisfy the quadratic
relationship (*), so the discriminant would have to be non-negative. However,
the student has shown that in fact the discriminant is negative.
must be non-negative. If there were
a solution x to your original equation, then the four numbers
x, a=1, b=-4, and c = 6 - sin x would satisfy the quadratic
relationship (*), so the discriminant would have to be non-negative. However,
the student has shown that in fact the discriminant is negative.
Here's another way to think about the student's answer. Suppose your
original equation had a solution x=r. That would mean
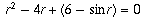 . Now, think of the quadratic
. Now, think of the quadratic
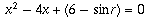 where r is just a fixed constant
and x is a variable not necessarily related to r. Now you have
a true quadratic function of x being set equal to zero.
The student has shown that this quadratic has no real roots
(no matter what value the constant r has, the discriminant will
always be negative). Since it has no roots at all, that proves that in
particular x=r is not a root, and hence it cannot be the case that
where r is just a fixed constant
and x is a variable not necessarily related to r. Now you have
a true quadratic function of x being set equal to zero.
The student has shown that this quadratic has no real roots
(no matter what value the constant r has, the discriminant will
always be negative). Since it has no roots at all, that proves that in
particular x=r is not a root, and hence it cannot be the case that
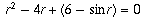 , no matter what r is.
, no matter what r is.
As for the question of "solving for x in terms of x": if you carry
out the derivation of the quadratic formula, it shows that if x, a,
b, and c are any four numbers related by the equation
 , then they are also related by the equation
, then they are also related by the equation
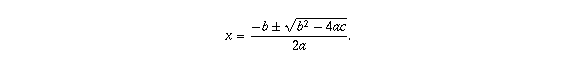
This is just a re-writing of the original equation by a process of completing the square.
Now, if the numbers a, b, and c happen to depend on x, as they do in your example, it is still legitimate to rewrite the equation as
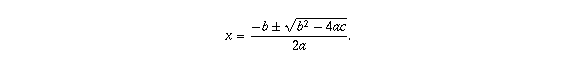
And, in the case of your example (where a=1, b=-4, and 6 - sin x), one can note that the term inside the square root is always negative, so the rewritten equation has no real solutions, so the original equation has no real solutions either.
The only difference between this case and the case where a, b, and c are constants is that here the rewritten form of the equation is not a solution for x, merely a different equation involving x. It is therefore of no use, except in theoretical arguments like this. However, in the case where a, b, and c are constants, the rewritten form of the equation is actually a solution for x in terms of a, b, and c.
Therefore, although the rewritten form of the equation is always valid, it is only a solution for x in the case in which a, b, and c are constants independent of x. It is usually only in this case that it is useful. Typically, students trying to apply it in other cases will do so incorrectly, but the student who answered your test question is a welcome exception!
This is just a follow up on a question I asked earlier about a "non-standard" solution to a quadratic equation problem. Thank you for your answer. I gave my student a printout of your argument and full marks for his solutions. However, just for the sake of playing "devil's advocate" here's another simmilar hypothetical problem and solution.The flaw in this second argument is the following. The fact that Delta > 0 means that the quadratic has solutions in the sense that there is a number y for whichDefine
on the domain {x : x>3}. Show that f(x) = 0 has real solutions.
Rewrite
. Delta = 4 - 4(6 - 2x)=8x - 20 > 0 since x > 3. Since Delta > 0, the quadratic has solutions.
Since there is nothing wrong with c = 6 - sin x, there should be nothing wrong with c = 6 - 2x.
Thank you again for answering my question.
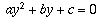 , i.e.,
, i.e., 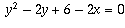 . However,
there is no reason why this root y should necessarily be the same thing
as the number x that occurs in the c coefficient, so it is not
legitimate to conclude from this that there is a solution x to the
equation
. However,
there is no reason why this root y should necessarily be the same thing
as the number x that occurs in the c coefficient, so it is not
legitimate to conclude from this that there is a solution x to the
equation 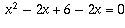 .
.
However, the first argument was correct because it showed that there
was no solution y at all to the equation 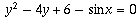 ,
and since there is no solution at all, in particular y=x cannot be a
solution.
,
and since there is no solution at all, in particular y=x cannot be a
solution.
Perhaps it might be useful to rephrase this in terms of the quadratic
formula. The original quadratic equation  can be rewritten as
can be rewritten as
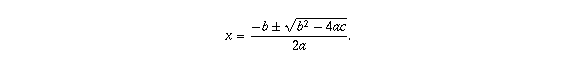
This rewriting is always valid.
Now, if a, b, and c are constants, this gives a solution for
x in terms of a, b, and c (or rather, two solutions); these solutions
are real numbers if and only if 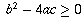 . Therefore, in the
case when a, b, and c are constants, the quadratic has real solutions
if and only if
. Therefore, in the
case when a, b, and c are constants, the quadratic has real solutions
if and only if 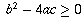 .
.
However, if a, b, or c is a function of x, then the rewritten
equation is simply a new, more complicated equation involving x.
If 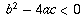 then clearly the equation can have no real solutions
because negative numbers do not have real-valued square roots. The
reverse implication, though, does not hold:
if
then clearly the equation can have no real solutions
because negative numbers do not have real-valued square roots. The
reverse implication, though, does not hold:
if 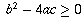 , that does
not necessarily mean there is a solution, only that a solution can
no longer be ruled out on such basic grounds.
, that does
not necessarily mean there is a solution, only that a solution can
no longer be ruled out on such basic grounds.
To put it yet another way: if 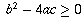 , then you can
certainly define a real number y by the formula
, then you can
certainly define a real number y by the formula
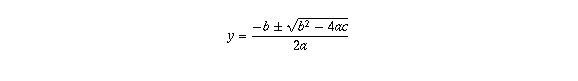
but there's no guarantee that this number y can be made to be the same number as the number x that occurs in the coefficients.
When the
coefficients are constants there is no such requirement; so in
the constant coefficient case you always get solutions when
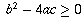 .
.
In the non-constant-coefficient case, you know there
cannot be solutions if 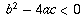 , but in the case
, but in the case
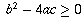 there is nothing about the rewritten equation that
allows you to easily tell if it has solutions or not.
there is nothing about the rewritten equation that
allows you to easily tell if it has solutions or not.
I hope this helps clear things up and I hope this makes for some useful discussions with your students.
![]() Go backward to Limit of the Sequence a(n) = cos(a(n-1))
Go backward to Limit of the Sequence a(n) = cos(a(n-1))![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Solution to a Functional Equation
Go forward to Solution to a Functional Equation![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page