(These buttons explained below)
Question Corner and Discussion Area
I was asked to proof that the midpoint formula of a line works. Obviously it works, but how do I go about proofing that. I started off with a line PQ at a slope, and formed a right triangle. Next, the point M is b/n P and Q, and I guess I'm trying to show M is in the middle. After this, I'm kinda lost, so anything to get me back on track will be appreciated.Suppose that P = (x,y) and Q = (X,Y) are the endpoints of our line segment. The midpoint M is then defined by M = ((x + X)/2,(y + Y)/2). To show that M is really the midpoint of the line segment PQ, we need to show that the distance between M and Q is the same as the distance between M and P and that this distance is half the distance from P to Q.Thanks in advance, I loved the work that you are doing here :-)
One approach is to use the distance formula to calculate the
relevant distances.
The distance between P and Q is
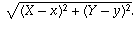The distances between M and P and M and Q are, respectively,
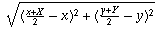and
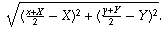Note that the distance from M to P simplifies to
become
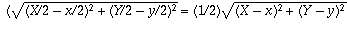which is just half the distance from Q to P.
It is easy to see that the same holds true for the distance from
M to P and therefore M is indeed the midpoint of the segment
PQ.
Another approach is to make use of similar triangles. Let M be the midpoint of the line segment PQ (i.e. the point which is exactly half way between the two points). Now draw vertical and horizonal lines through all of the points. We will assume here that PQ is neither vertical nor horizontal, since it is simple to show that the midpoint formula is true for horizonal and vertical line segments.
The horizonal line though P and the vertical line through Q will meet at a unique point R. Similarly the horizontal line through M meets the vertical line through Q at a single point A and the horizontal line through P meets the vertical line through M at a single point B.
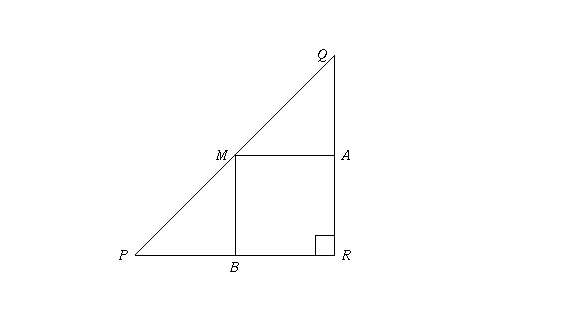
Note that PMB and MQA are similar triangles. Since |PM| = |MQ| (because M is the midpoint of PQ), they are congruent triangles. Thus |PB| = |MA| = |BR| so B is the midpoint of PR, and similarly A is the midpoint of QR.
The x-coordinate of M equals the x-coordinate of B. Assuming R is to the right of P as in the picture, this equals the x-coordinate of P plus |PB|, which is x + |PB| = x + (1/2)|PR| = x + (1/2)(X-x) = (x+X)/2. (If R is to the left of P, so is B, and we get the x-coordinate of M equal to x - |PB| = x - (1/2)|PR| = x + (1/2)(x-X) = (x+X)/2).
A similar argument shows the y-coordinate of M equals (y+Y)/2.
Go backward to Questions about Slopes and Lines Go up to Question Corner Index Go forward to Infinity, Pi and Symmetry Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page