Question Corner and Discussion Area
Question Corner and Discussion Area
I am interested in knowing what i to the power of i is.The first question to address is what it means to raise one complex number to the power of another. There is a basic definition of what it means to raise e to a complex power, as described in the answer to an earlier question. Therefore, if z is any complex number for which
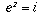 ,
,
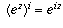 is a possible value for
is a possible value for 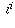 .
.
What are the possible values for z? Well, if we write z = a + bi,
then 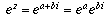 . By
de Moivre's theorem (explained in the answer to an earlier question),
. By
de Moivre's theorem (explained in the answer to an earlier question), 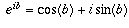 , so
, so
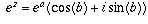 . This expression equals i
exactly when a=0, cos(b)=0, and sin(b)=1. This occurs when
. This expression equals i
exactly when a=0, cos(b)=0, and sin(b)=1. This occurs when
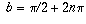 for some integer n, so the possible values of
z are
for some integer n, so the possible values of
z are 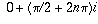 .
.
Therefore, the values of 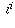 are
are
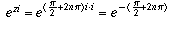
for any integer n.
Note that there is more than one value
for 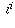 , just as 2 and -2 are both square roots of 4.
(However, while the square roots of a number always have the same
magnitude even if they differ in sign, the values of
, just as 2 and -2 are both square roots of 4.
(However, while the square roots of a number always have the same
magnitude even if they differ in sign, the values of 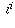 have
different magnitudes).
The
principal value of
have
different magnitudes).
The
principal value of 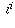 would be
would be 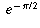 --the case where
n=0.
--the case where
n=0.
It's also interesting to note that all these values of 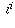 are
real numbers.
are
real numbers.
![]() Go backward to What is the Square Root of i?
Go backward to What is the Square Root of i?![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Raising a Number to a Complex Power
Go forward to Raising a Number to a Complex Power![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page