(These buttons explained below)
Question Corner and Discussion Area
How do you graph an inverse function once you have solved it?It is actually easier to graph the inverse of a function than it is to solve for it.
First let's think about what it means to graph a function.
Suppose that we wanted to graph a function f(x).
To do this, we would substitute numerical values for x and
plot those ordered pairs (x,y) for which y=f(x).
For instance, if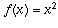 
, we might
try plotting the points (0,0), (1,1), (2,4), (3,9), etc.
Now how would we plot the inverse of a function? If g is the inverse function of f, then to graph g we'd plot the points (x,y) where y=g(x). This condition is the same as the condition x=f(y), so the graph of the inverse consists of points (f(y),y).
These are the same as the points on the graph of f but with the
order of the coordinates interchanged:
instead of plotting (x,f(x)) for various numerical values of
x, we plot (f(y),y) for various numerical values of y
(which is the same thing as plotting (f(x),x) for various numerical
values of x).
For example, some of the points on the graph of the inverse of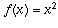
are (0,0), (1,1), (4,2), and (9,3).
Geometrically, we have just reflected the graph of the function
f(x) through the line y=x to get the graph of the inverse of f(x).
This method of graphing the "inverse" of a function always works, even
when the function doesn't have an inverse.
If the function doesn't have an inverse, it is because there are two
distinct values a and b which we can assign to x to get the
same value for f(x).
If we examine our function 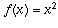we will note that
f(2) = f(-2) = 4.
The corresponding points on the graph of our "inverse
function" are (4,2) and (4,-2).
Thus the graph which we constructed in this method is not really the
graph of a function, since the value of the inverse of f(x) is
not well defined at 4 (it could either be 2 or -2).
Even though this approach will not always give us the graph of a function, it will whenever the inverse of f(x) exists.
Go backward to Multiplying Matrices Go up to Question Corner Index Go forward to Does Every Function Have an Antiderivative? Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page