(These buttons explained below)
Question Corner and Discussion Area
Hi!One good way to tackle this problem is to ask the following question:My name is Krishna. Before when I was in the math club, they posed a question. The question is:
what is the 'sqrt[1+sqrt 1+sqrt 1 ........ ?
The square root is abbreviated with 'sqrt'. Also note that the sqrt sign is within the sqrt sign and so on.
Thank you.
Krishna.
Assuming this number exists, is there an equation that it must satisfy, an equation which is simple enough that it can be easily solved?If we let x denote this number, notice that we have
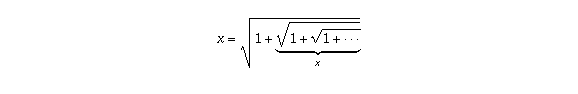
and the part underlined with a brace
is the same thing
as x itself. This means that x must satisfy the equation
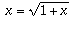which can be solved by squaring both sides to get x^2 = 1 + x, using
the quadratic formula to find
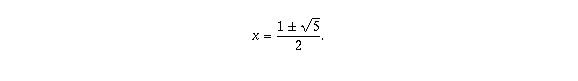
Since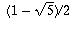 
is negative, but x is positive, x has to be the
other root, namely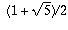 
.
What this method does is it tells you that, if such a number x exists, then you can figure out what it has to be.
That's probably all you were asking for, but strictly speaking it isn't a complete answer. It leaves open the question: Does this number exist at all?
To prove that it does, you need some ideas from calculus: every bounded, increasing sequence has a limit. Here we are looking for the limit of the sequence
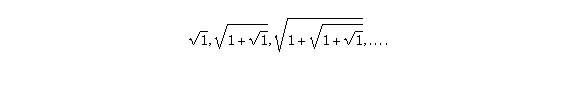
Can you show that this sequence is bounded and increasing? (Hint: you will need to use mathematical induction. Boundedness is the trickiest one to prove; try proving by induction that all of the terms are less than 2. Use the fact that the nth term a(n) and (n-1)st term a(n-1) are related by
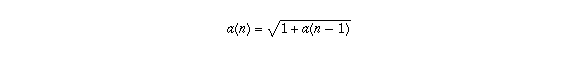
to show that, if a(n-1) is less then 2, then a(n) must be also).
Post another question if you want more of an answer on this part!
Go backward to Recent Questions Go up to Question Corner Index Go forward to Finding the Sum of a Power Series Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page