Question Corner and Discussion Area
Question Corner and Discussion Area
I would like to know the three ancient impossible constructions problems using only a compass and a straight edge of Euclidean Geometry.The three problems are:
People tried for centuries to find such constructions. It was not until the development of "abstract algebra" in the nineteenth century that it was proven these constructions were impossible.
For those of you who are interested, the basic idea of the proof is as follows.
Since the only shapes you can draw with a compass and straightedge are line segments and circles (or parts of circles), the only ways of constructing new points out of old points to to take the intersection of two lines, two circles, or a line and a circle. Now, if you write down the general equations for these intersections and try to solve for one of the coordinates of the intersection point, you will end up with either a linear or quadratic equation. The coefficients of the equation involve the coordinates of the old points (or various sums, differences, products, or quotients of them).
Linear equations can be solved by simple division: the equation ax = b has as its solution x = b/a. Quadratic equations can be solved using the quadratic formula. In each case, we see that the only arithmetic operations required to calculate the new coordinate from the old coordinates are addition, subtraction, multiplication, division, and taking square roots.
Therefore, if you start with some initial points whose coordinates are all rational numbers, then apply any sequence of compass-and-straightedge construction techniques, the coordinates of the points you end up with will be a very special kind of number: they will be obtainable from the rational numbers by a sequence of operations involving only addition, subtraction, multiplication, division, and the extraction of square roots.
The reason the three classical constructions are impossible is that they are asking you to be able to construct points whose coordinates are not numbers of this type.
Proving that they are not numbers of this type requires some very advanced mathematics from an area called Field Theory. I'll sketch some of the essential ideas.
The key theorem is this:
If x is a number obtainable from the rationals using only addition, subtraction, multiplication, division, and the taking of square roots, then x is a solution to some polynomial equation with rational coefficients. Moreover, if one factors out irrelevant factors from this equation until one gets down to an "irreducible" polynomial equation (one that can't be factored any further and still have rational coefficients), the degree of this polynomial will always be a power of 2.Intuitively speaking: each time you take a square root, you usually double the degree of the polynomial required to represent the number. For example,
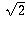 can be represented as a solution to the
quadratic equation
can be represented as a solution to the
quadratic equation 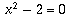 , whose degree is 2. (Of course,
it's also a solution to
the cubic equation
, whose degree is 2. (Of course,
it's also a solution to
the cubic equation 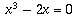 whose degree is 3, not a power of 2;
but that's because this equation can be factored, and after factoring out
the redundant factor of x you are left with the quadratic
whose degree is 3, not a power of 2;
but that's because this equation can be factored, and after factoring out
the redundant factor of x you are left with the quadratic
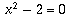 , which is irreducible: it can't be factored any further
and still have rational coefficients). If we take a square root a second
time, getting the number
, which is irreducible: it can't be factored any further
and still have rational coefficients). If we take a square root a second
time, getting the number 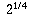 , it's a root of the
fourth-degree
polynomial
, it's a root of the
fourth-degree
polynomial 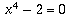 (which is irreducible).
A number like
(which is irreducible).
A number like 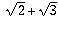 ,
also obtained by twice taking a square root, is also the
root of an irreducible fourth-degree polynomial:
,
also obtained by twice taking a square root, is also the
root of an irreducible fourth-degree polynomial:
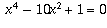 . A number obtained by taking a square root
three times, like
. A number obtained by taking a square root
three times, like 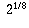 , is typically the root of an irreducible
8th degree polynomial, like
, is typically the root of an irreducible
8th degree polynomial, like 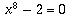 .
.
This intuitive understanding is not always correct, though. For example,
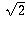 +
+ 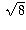 , even though it is obtained using two
square roots, is the same as
, even though it is obtained using two
square roots, is the same as 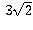 , which involves only one
square root. So the intuitive argument only serves to show you that the
claims of the theorem are reasonable. Actually proving the theorem
(and proving, not just that there's some irreducible polynomial
equation for x whose degree is a power of 2, but that
every irreducible polynomial equation for x also has that same
degree) involves many advanced ideas.
, which involves only one
square root. So the intuitive argument only serves to show you that the
claims of the theorem are reasonable. Actually proving the theorem
(and proving, not just that there's some irreducible polynomial
equation for x whose degree is a power of 2, but that
every irreducible polynomial equation for x also has that same
degree) involves many advanced ideas.
Using the theorem, it is easy to prove the impossibility of the three constructions:
Doubling a cube is impossible because if you start with a cube of side
length 1, you would need to cunstruct a cube whose side length is the
cubed root of 2. But the the cubed root
of 2 is a solution to the irreducible equation 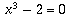 whose
degree, 3, is not a power of 2.
whose
degree, 3, is not a power of 2.
Squaring a circle is impossible because if you start with a circle of
radius 1 you would need to construct a square whose side length is
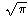 . But this is a so-called "transcendental number": it is
not the solution to any polynomial equation with rational
coefficients, let alone one whose degree is a power of 2.
. But this is a so-called "transcendental number": it is
not the solution to any polynomial equation with rational
coefficients, let alone one whose degree is a power of 2.
Trisecting an angle is impossible because if you start with an angle
of 60 degrees (which is easily constructible), you would then need to
be able to construct an angle of 20 degrees. This would be equivalent
to constructing a point whose coordinates are the cosine and sine of
20 degrees. This is impossible because cos(20 degrees) is a
solution to the irreducible
polynomial equation 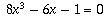 whose degree, 3,
is not a power of 2.
whose degree, 3,
is not a power of 2.
![]() Go backward to Constructing a Pentagon
Go backward to Constructing a Pentagon![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Using Geometric Postulates for Theorems in 3 Dimensions
Go forward to Using Geometric Postulates for Theorems in 3 Dimensions![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page