Question Corner and Discussion Area
Question Corner and Discussion Area
Hello. I would like to know about hypercomplex numbers (of the form a + xi + yj), their properties and rules (addition, subtraction, multiplication, division, etc). In what areas are they useful ? Give me some examples if possible.The hypercomplex numbers are a generalization of the complex numbers. They were created in an attempt to describe certain geometric operations in spaces with a dimension higher than the 2-dimensional plane.
Operations on the complex numbers can be used to describe many of the geometric operations on the plane. For instance multiplication by a real number corresponds to a scaling of the plane. Multiplication by complex numbers with a modulus ("length") of 1 corresponds to a rotation of the plane. Adding complex numbers corresponds to translation of the plane. More examples are available on the geometry and imaginary numbers page.
It was wondered for some time whether this could be generalized to 3-dimensional space (that is, to numbers of the form a + xi + yj, which is what you were asking about). It is known now that this is not possible. The only dimensions in which there are hypercomplex numbers which allow for a notion of division are dimensions 4 and 8. These hypercomplex numbers are called the Quaternians and Octonians respectively (the Quaternians are sometimes called Hamilton Numbers and the Octonians are often called Cayley Numbers).
In both cases these number systems are unique - the only numbers with these geometric properties in dimension 4 are the Quaternians and in dimension 8 are the Cayley Numbers. Also, with increases in dimension, we can not maintain some of the properties which make number systems simple. In both the Quaternians and the Cayley numbers, multiplication is non-commutative. That is that if a and b are two numbers, then (a)(b) need not be the same number as (b)(a). In that case of the Cayley Numbers, multiplication is not even associative. By this we mean that if a, b, and c are three Cayley numbers, then it is not always true that (ab)c is the same number as a(bc) (here the parentheses tell us which operation to perform first).
While the definition of the Cayley Numbers is quite elaborate, the Quaternians can be defined without too much trouble. There are three Quaternians which, together with the Real numbers, generate all of the others. They are given the names i, j, and k. A typical example of a Quaternian is 1 + 3.3i + 9j - 1.5k.
Addition is defined as you would define addition on a polynomial with variables i, j, and k. For example, the sum of 1 + 5j and 2 + 4j + 13k is 3 + 9j + 13k.
Multiplication is also defined just like multiplication on polynomials
except that we are allowed to make certain simplifications:
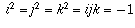 .
We can derive other relations, such as i = jk, from the ones given above.
Thus (1 + 5j)(2 + 4j + 13k) equals
.
We can derive other relations, such as i = jk, from the ones given above.
Thus (1 + 5j)(2 + 4j + 13k) equals
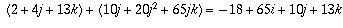 .
.
The addition and multiplication of hypercomplex numbers are always defined in the same way, regardless of the dimension. What defines the behavior of the system is the rules for simplification. Other, more obscure hypercomplex number systems exist and are generally based around the multiplication of certain types of matrices. These, however, fail to have a notion of "division" and are more difficult to work with.
![]() Go backward to What are the Origins of Number Systems?
Go backward to What are the Origins of Number Systems?![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Why is the Product of Negative Numbers Positive?
Go forward to Why is the Product of Negative Numbers Positive?![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page