(These buttons explained below)
Question Corner and Discussion Area
For every fuction with symmetry will the first derivative have symmetry of the other type? What Theorem proves this if it is in fact true?Yes, it is true. If f is an even function (that is, has the same value if you replace x by -x), then its derivative will be an odd function (changes sign when you replace x by -x), and vice versa.
This is quite clear geometrically; in the picture below, for example, it is apparent that the slopes m and M are negatives of each other. You could even turn this into a geometric proof: if f is even, its graph is the same if you reflect it in a mirror placed along the y-axis, and therefore the tangent line at one point is the mirror reflection of the tangent line at the reflected point, and a line reflected in the y-axis has its slope multiplied by -1.
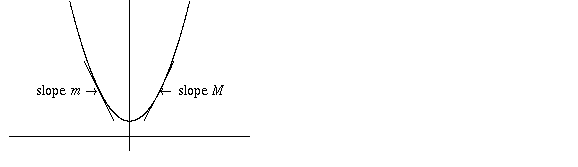
In the above picture, m = -M.
The way that you prove it using only calculus theorems (without needing any geometry at all) is as follows.
If f is an even function, that means that f(x) = f(-x).
Now differentiate both sides. The left-hand side becomes f'(x), and the right-hand side becomes -f'(-x) (using the chain rule).
Therefore, f'(x) = - f'(-x). In other words, the value of f' at x is the negative of its value at -x, so f' is an odd function.
Similarly, if you started with an odd function f, you have f(x) = - f(-x). Differentiating both sides gives f'(x) = + f'(-x), so f' is an even function.
In either case, f' has the opposite type of symmetry (even or odd) from f.
Go backward to Does Every Function Have an Antiderivative? Go up to Question Corner Index Go forward to Factorials of Non-Integral Values Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page