How To Express A Repeating Decimal Number As A Fraction

Asked by Dana Shaddad, student, Qatar International on September 22, 1997:

How do you find a rule for expressing any recurring decimal as a fraction and such rule to be tested with examples of three digits, four digits, five digits repeating patterns.

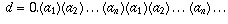
There is a rule for converting a repeating decimal number into a fraction. Let's first of all suppose that the repeating pattern starts immediately after the decimal point, with zero before the decimal point. Let's say the repeating part is n digits long, so the number looks like (IMAGE)

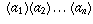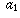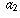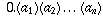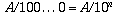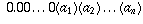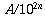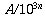Let A stand for the integer (IMAGE) (the n-digit number whose n digits are (IMAGE) , (IMAGE) , etc.). Then the first part of of our number, (IMAGE) , is the same as (IMAGE) . The next part of our number is (IMAGE) , which is (IMAGE) . The next part is (IMAGE) , and so on.

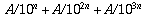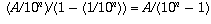This means that our number d is equal to the infinite sum (IMAGE) . This is a geometric series and by a well known formula (as described in another question) its value is (IMAGE) .

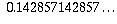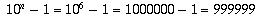To see that this formula works, consider the decimal (IMAGE) . In this case A=142857, n=6, and (IMAGE) . Then this decimal is equal to 142857/99999. This fraction then reduces to 1/7.

If you have a decimal where the repeating part doesn't start right after the decimal point, first multiply or divide by 10 enough times so that the repeating part does start right after the decimal point, then undo your multiplication or division at the end.

For example, suppose you have the decimal d=3.4575757. . . . Multiply by 10 to get 10 d = 34.575757. . . . Our formula tells you that the 0.575757. . . part equals 57/99, so 10 d = 34 + 57/99, and therefore d = 34/10 + 57/990.

Asked by Peter Collins, student, Mill Hill School on January 2, 1998:

How can you calculate what a fraction will be in decimal form? More specifically: How can you tell if a fraction is a recurring decimal or not, and if it is what will be the value of the decimal? (without a calculator).
This is in relation to the question posted in September about writing a decimal in fractional form.

To calculate a fraction in decimal form, you perform long division. You should be familiar with this procedure from early arithmetic lessons. For example, to calculate 3/11, you say that 11 goes into 3 zero times, with remainder 3. So the answer starts 0. Then you find that 11 goes into 30 two times, with remainder 8. So the answer starts 0.2. Next you find that 11 goes into 80 seven times, with remainder 3. So the answer starts 0.27. Now that you have a remainder 3 which you have seen before, you see that the pattern will repeat: 0.272727. . . .

Every fraction produces a recurring decimal. That is because there are only a finite number of possibilities for the remainder, so eventually you will encounter a remainder you have seen before, and the pattern of digits will continue from that point on.

Some fractions will give you a decimal where the recurring part is all zeros, such as 4/5 = 0.80000. . . = 0.8. Such decimals are called terminating decimals. The fractions which give you terminating decimals are those which can be written in a form where the denominator is a power of 10 (for example, 4/5 = 8/10). Which fractions can be written this way? Precisely those fractions for which, when you write them in lowest terms (factoring out any common factors from top and bottom), have the property that the denominator is a product of 2's and/or 5's but no other prime factors. Then you can multiply top and bottom by an appropriate number of 2's and 5's to get a power of 10.

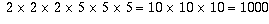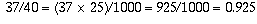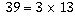For example, 37/40 will give you a terminating decimal, because 40 is 2 times 2 times 2 times 5. If you multiply top and bottom by two more 5's, i.e. by 25, then the denominator will become (IMAGE) so (IMAGE) . (This is the same answer you would get if you carried out the long-division procedure above). However, 32/39 will give you a non-terminating decimal because, even though it is in lowest terms, the denominator (IMAGE) has prime factors other than 2 and 5, so there is nothing you could multiply it by to get a power of ten.

[ Submit Your Own Question ] [ Create a Discussion Topic ]

This part of the site maintained by (No Current Maintainers)
Last updated: April 19, 1999
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel:

$(SWITCH TO TEXT-ONLY VERSION)$

Go backward to Why is x^0 = 1?
Go up to Question Corner Index
Go forward to Published Proof of Fermat's Last Theorem
$(SWITCH TO TEXT-ONLY VERSION)$ Switch to text-only version (no graphics)
Access printed version in PostScript format (requires PostScript printer)
Go to University of Toronto Mathematics Network Home Page