Question Corner and Discussion Area
Question Corner and Discussion Area
In my math class, our teacher has given us an independent study on sequences and series. This is one question for example: A superball bounces to 3/4 of its initial height when dropped on dry pavement. If the ball is dropped from a height of 16 metres,A good place to start is to think of how high the ball goes on each bounce. This gives you a sequence: a(0) is height from which ball was dropped (16), a(1) is the height of the first bounce, which is 3/4 of a(0), a(2) is the height of the second bounce, and so on. Your questions are to (a) find a(5), and (b) find the sum of a(0) (amout it falls initially) plus 2 a(1) (amount it goes up and down after hitting the ground the first time), plus 2 a(2), and so on, up to 2 a(5).a)How high does it bounce after the fifth bounce?
b)How far does the ball travel by the time it hits the ground for the sixth time?
Please help me answer this question as soon as possible. This may be an easy question for you since you probably are used to dealing with complex questions and intelligent students but could you please just help me out with this one? Thank you!
Respectfully,
Melanie Graine
Grade 11 student at K-OAC High School
The information you have about the sequence is that each bounce is 3/4 the height of the previous bounce. This tells you that a(n+1) = 3/4 a(n). So you can now calculate a(1) = (3/4) a(0) = (3/4) 16 = 12, a(2) = (3/4) a(1) = (3/4) (12) = 9, and so on. Then you can answer the questions asked.
More interesting are the questions "how long will the ball keep bouncing, and how far will it go in total?" Even if it makes an infinite number of bounces, the total time taken, and the total distance travelled, will be finite! To answer these questions you need a formula for a(n), which you can get by writing
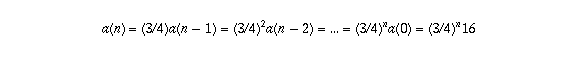
Then the total distance travelled can be found by taking the sum of this infinite series (actually, you need to take twice the sum less the first term, since on all bounces except the initial drop the ball has to go both up and down). The way you find the sum of an infinite series like this is described in the answer to another question; the answer turns out to be exactly 112 metres.
The fact that the total time taken is finite requires some knowledge of physics to calculate the time travelled for each bounce, but you end up with a similar series that has a finite sum.
![]() Go backward to Numbers Defined By Infinite Sums
Go backward to Numbers Defined By Infinite Sums![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Angle Between Vertices of a Tetrahedron
Go forward to Angle Between Vertices of a Tetrahedron![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page