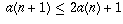Go backward to Discovering the Mathematics Behind the Game Go up to The Tower of Hanoi Go forward to The Answer Switch to text-only version (no graphics) Go to University of Toronto Mathematics Network
Home PageIn other words: if a(n) is the minimum number of turns it takes to move n disks from one post to another, then a(n+1) = 2 a(n) + 1.
Hold on a minute. This isn't quite right. It just means you can move
n+1 disks in 2 a(n) + 1 turns. But is this the minimum
number of turns, or can you do it in fewer? All we've really proven is
that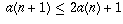 
.
See if you can prove that it really is the minimum number of turns. (Hint: the bottom disk will have to be moved at some point. What must happen before the bottom disk can be moved? What's the smallest number of turns this could possibly take? What must happen after the bottom disk is moved? What's the smallest number of turns this could possibly take?)
Tying this in to the pattern. Our formula a(n+1) = 2 a(n) + 1 is great, but the pattern we want is something that says what a(n) is in terms of n. You should have conjectured that a(n) = f(n) where f(n) is some explicit function of n that you wrote down. How can you tell if your conjecture is right or not?
Note: If you couldn't conjecture a formula for f(n) before, you may be able to do so now, because now you have more numbers to work with! Before we knew that the number of turns required for 1, 2, 3, and 4 disks were 1, 3, 7, and 15. But now we can also figure out the number of turns for 5 disks ((2)(15) + 1 = 31), the number of turns for 6 disks ((2)(31) +1 = 63), and so on. Can you see a pattern to the numbers 1, 3, 7, 15, 31, 63, . . . ? Try adding 1 to them all. Now you should be able to make a conjecture. How can you tell if it's right or not?
The answer: try to prove it by induction. First, show that it's true for n=1: show that a(1) = f(1). Next, show that, if it's true for n=k, then it's also true for n=k+1. In other words, assume that a(k) = f(k). Now try to show that a(k+1) = f(k+1).
You can do this by using the fact that a(k+1) = 2 a(k) + 1 = 2 f(k) + 1, so you just have to make sure that 2 f(k) + 1 is the same as f(k+1). This you can do just by using your formula for what f(k) is, and checking that 2 f(k) + 1 = f(k+1).
(If you were unable to make a conjecture for what the formula should be, the answer is given in the next section. But the task of proving that it's true is left up to you!)
Back to the Legend. Now we know the minimum number of turns required to move n disks. If the monks work fast and move one disk every second, how many years will it take them to finish the job? Are you surprised by your answer? Do you think the chilling prophecy is likely to be true?