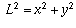Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)
(IMAGE) Go backward to This is Not the Fallacy
(IMAGE) Go up to A Ladder Will Fall Infinitely Fast when Pulled
(IMAGE) Go forward to This is Not the Fallacy
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Go to University of Toronto Mathematics Network Home Page

Congratulations; you have correctly identified the fallacious step!

There is the implicit assumption here that the top of the ladder remains resting against the wall. However, that is not always true. Once the ladder has reached a sufficiently small angle to the horizontal, your pulling of the bottom away from the wall will actually cause the top to pull away from the wall too. When this happens, there is no longer the relationship (IMAGE) , because x, y, and L no longer form the sides of a closed right triangle.

If you want to verify this for yourself, just try it out on your favourite ladder. You will see that the top pulls away from the wall just before the ladder becomes horizontal.

To understand mathematically (or rather, physically) why this is true, suppose for a moment that there was no gravity. Then, when you pull the ladder, you will pull the entire ladder as a unit, with both top and bottom moving away from the wall with the same speed.

The only reason the top stays in contact with the wall for most of the time is because of gravity. If the wall were not there, gravity would cause the top of the ladder to fall to the ground in a path like that indicated below:

(IMAGE)
Therefore, the effective force of gravity on the top of the ladder (actually, the combination of gravity and the rigidity of the ladder that prevents the ladder from shrinking in length and collapsing in a heap) is as shown in the diagonal purple arrow in the picture below. This effective force can be thought of as the sum of two forces (the horizontal and vertical blue arrows): one that pushes the top of the ladder against the wall, and one which slides the top of the ladder down the wall.
(IMAGE)
As the ladder gets more and more horizontal, the effective force acting on the top of the ladder (the diagonal arrow) becomes closer to vertical, and the force pushing the top against the wall will become less and less, as you can see from the shortening of the horizontal arrow between the above picture and the one below:
(IMAGE)
Once the force pushing the top of the ladder against the wall becomes less than the force with which you are sliding the bottom of the ladder away from the wall, your force will prevail and you will pull the ladder away from the wall. Once this happens, the top will be in free-fall and no longer governed by the same set of equations.

A good exercise is to try to figure out the equation for the position of the top of the ladder during this free-fall stage.

To see the explanations for the other steps, finding out exactly why they're correct (or, in some cases, finding out which other steps have slight mistakes in them), go back to the list of steps in the proof. To try your hand at finding the fallacy in a different problem, go back to the Classic Fallacies index page.
This page last updated: May 26, 1998
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)