Answers and Explanations
Answers and Explanations
Yes, there does exist an object one could call "infinity" in the sense that it measures the size of the infinite set {1, 2, 3, . . . } in the same way that an ordinary natural number measures the size of a finite set.
One way to see that there does in fact exist an object that can serve as a measure of the size of a set is just to use the collection of all sets of that size as your object. For example, the number "1" can be defined as the collection of all the single-element sets in the world, the number "2" can be defined as the collection of all pairs of things in the world, and so on. (This may sound like a circular definition but that's just because I've been oversimplifying a bit). In a similar way, one can define the "size" of the infinite set {1, 2, 3, . . . } to be the collection of all the sets in the world that have the same size as this set.
So, if one asks the question does there exist any object that one can call "infinity", in the sense that it measures the size of the infinite set {1, 2, 3, . . . } in the same way that an ordinary natural number measures the size of a finite set, the answer is yes. However, we really shouldn't use the word "infinity" for this one object alone, because there are other infinite sets with different sizes. This is an interesting topic, so we will discuss it briefly. Many infinite sets have the same size. For instance, the set of even integers has the same size as the set of all integers. In one sense that may seem surprising, since the second set has all the elements of the first set in it plus all the odd integers as well, but it's fact of life about infinite sets that you can add elements to an infinite set without altering its size. But in another sense it's not surprising at all that, since both sets are infinite, their sizes should each be the same "infinity" concept.
What is really surprising is that there are other infinite sets which do not have the same size as the set of integers! For instance, the set of all real numbers is a much bigger set. So the "infinity" concept that describes the size of the set of real numbers is a different one from the one which describes the size of the set of integers. In other words, in the context of measuring sizes of sets there is no one single "infinity" concept, but lots of different ones appropriate to the different possible sizes.
These concepts that describe the sizes of infinite sets are called
infinite cardinal numbers. The size of the set of integers
(which is the same as the size of the set of even integers, which is
the same as the size of the set of odd intgers, which is the same as
the size of the set {1, 2, 3, . . . } of natural numbers, and so
on) is called 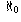 (pronounced
"aleph-null"); it's the Hebrew letter Aleph with a zero
subscript. There are also different cardinal numbers that describe the
sizes of sets (such as the set of real numbers) that are not the same
size as the set of integers. There are in fact infinitely many
different infinite cardinal numbers!
(pronounced
"aleph-null"); it's the Hebrew letter Aleph with a zero
subscript. There are also different cardinal numbers that describe the
sizes of sets (such as the set of real numbers) that are not the same
size as the set of integers. There are in fact infinitely many
different infinite cardinal numbers!
![]() Go backward to Topological Context: Why Infinity Does Exist
Go backward to Topological Context: Why Infinity Does Exist![]() Go up to Does "Infinity" Exist?
Go up to Does "Infinity" Exist?![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page