(These buttons explained below)
Answers and Explanations
one gets
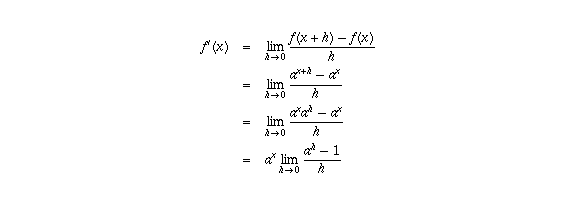
which is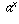 
times a number (the limit of
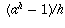as h goes to 0) which is a constant
independent of x, depending only on the base a
of the exponential.
Therefore, the derivative of an exponential function is just a constant times the function value. What the constant is depends on what the base of the exponential function is.
The number e is that value of the base
which yields the constant 1, so that the derivative of the function
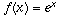is actually equal to 
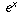itself.
Moreover, the derivative of the more general function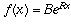 
is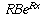 
. If we were
using some other number a as the base instead of e, there would be
an additional constant out front.
Not only does this make it more natural and convenient to use e
as the base in exponentials and logarithms, but it relates back to the
compound interest interpretation given earlier. If a bank account is
growing under compound interest, with an interest rate of R per
unit time, that means that at any instant in time the growth rate is
R times the current balance. We've already seen that the
balance at the end of the period is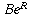 
where B is the
beginning balance. More generally,
to figure out the balance somewhere in the middle of the time period,
let t denote the fraction of the time period that has passed;
it turns out that the balance at that time is
.
The derivative of this function is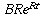 
which is
R times the function value; this is just another way of saying
that the growth rate is R times the current balance.
Go backward to The Number e as a Limit Go up to Does the Number e Have Special Meaning? Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page