|
|
|
|
Geometry, the study of shapes, form the basis of much of the
mathematical curriculum from elementary schools through
universities. There is so much more than this, however, from tilings
of the plane to minimal surfaces, from non-Euclidean geometries (like
hyperbolic space) to non-orientable surfaces (like the Möbius
strip or Klein bottle). Much of the study of these topics is
accessible to a high school student willing to visualize.
|
|
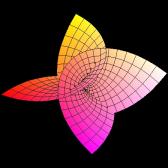
This is what's known as a minimal surface. These surfaces
generalize the behaviour of soap film or bubbles. A bent wire
dipped in a soap solution will form a soap film, and this film is
the smallest (in terms of area) such film that will bound this
wire. The figure at the right is not a soap film, but instead is a
surface that has the same local shape as a film. It is a classic
surface known as Enneper's surface.
|
|
|
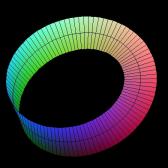
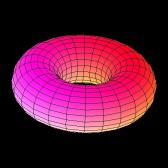
This video game universe has the same shape as a donut. The picture
to the left is what a mathematician would call a torus. The
game, by identifying opposite vertical sides, turns the universe into
a cylinder. By then identifying the top and bottom sides, the game
has wrapped this cylinder into the donut-shape shown.
|
|
|
Our approach is motivated by mathematics research. We will search for
patterns in hands-on examples and discover (and prove) rules based on
these patterns. The study of geometry allows us to ground our
abstract results in terms of straightforward examples; that is, our
mathematically rigorous results will come from experimenting with
shapes via problem-solving, games, and computer programs.
|
|
|