
$\renewcommand{\Re}{\operatorname{Re}}$ $\renewcommand{\Im}{\operatorname{Im}}$ $\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\dag}{\dagger}$ $\newcommand{\const}{\mathrm{const}}$ $\newcommand{\arcsinh}{\operatorname{arcsinh}}$
In this Chapter we consider simplest separation of variables problems, arising simplest eigenvalue and eigenfunction problems, and the corresponding Fourier series.
Consider IBVP for homogeneous 1D-wave equation on the finite interval $(0,l)$: \begin{align} & u_{tt}-c^2 u_{xx}=0,&& 0< x< l, \label{eq-4.1.1}\\[3pt] & u|_{x=0}=u|_{x=l}=0, \label{eq-4.1.2}\\[5pt] & u|_{t=0}=g(x), \quad u_t|_{t=0}=h(x).\label{eq-4.1.3} \end{align} Note, that boundary conditions are also homogeneous. So inhomogeneous are only initial conditions.
Let us skip temporarily initial conditions (\ref{eq-4.1.3}) and consider only (\ref{eq-4.1.1})--(\ref{eq-4.1.2}) and look for a solution in a special form \begin{equation} u(x,t)= X(x) T(t) \label{eq-4.1.4} \end{equation} with unknown functions $X(x)$ on $(0,l)$ and $T(t)$ on $(-\infty,\infty)$.
Remark 1. We are looking for non-trivial solution $u(x,t)$ which means that $u(x,t)$ is not identically $0$.
Therefore neither $X(x)$ nor $T(t)$ could be identically $0$ either.
Plugging (\ref{eq-4.1.4}) into (\ref{eq-4.1.1})--(\ref{eq-4.1.2}) we get \begin{align*} & X(x) T''(t)=c^2 X''(x)T(t), \\[3pt] & X(0)T(t)=X(l)T(t)=0, \end{align*} which after division by $X(x)T(t)$ and $T(t)$ respectively become \begin{align} & \frac{ T''(t)}{T(t)}=c^2 \frac{X''(x)}{X(x)}, \label{eq-4.1.5}\\[3pt] & X(0)=X(l)=0. \label{eq-4.1.6} \end{align} Recall, neither $X(x)$ nor $T(t)$ are identically $0$.
In (\ref{eq-4.1.5}) the l.h.e. does not depend on $x$ and the r.h.e. does not depend on $t$ and since we have an identity we conclude that
Remark 2. Both expressions do not depend on $x,t$ and therefore they are constant.
This is a crucial conclusion of the separation of variables method. We rewrite We rewrite the (\ref{eq-4.1.5}) as two equalities \begin{equation*} \frac{T''(t)}{T(t)}=-c^2\lambda,\qquad \frac{ X''(x)}{X(x)}=-\lambda, \end{equation*} with \alert<2>{unknown constant $\lambda$}, which in turn we rewrite as (\ref{eq-4.1.7}) and (\ref{eq-4.1.8}): \begin{align} &X'' +\lambda X=0, \label{eq-4.1.7}\\[3pt] & X(0)=X(l)=0, \tag{\ref{eq-4.1.6}}\\[5pt] & T''+ c^2\lambda T=0.\label{eq-4.1.8} \end{align}
Consider BVP (for ODE) (\ref{eq-4.1.7})--(\ref{eq-4.1.6}). It is usually called Sturm-Liouville problem. We need to find its solution $X(x)$ which is not identically $0$.
Definition 1. Such solutions are called eigenfunctions and corresponding numbers $\lambda$ eigenvalues (compare with eigenvectors and eigenvalues).
Proposition 1. Problem (\ref{eq-4.1.7})--(\ref{eq-4.1.6}) has eigenvalues and eigenfunctions \begin{align} & \lambda_n = \frac{\pi^2n^2}{l^2}&& n=1,2,\ldots, \label{eq-4.1.9}\\[3pt] &X_n(x)=\sin (\frac{\pi n x}{l}). \label{eq-4.1.10} \end{align}
Proof. Note that (\ref{eq-4.1.7}) is a 2-nd order linear ODE with constant coefficients and to solve it one needs to consider characteristic equation \begin{equation} k^2+\lambda =0 \label{eq-4.1.11} \end{equation} and therefore $k_{1,2}=\pm \sqrt{-\lambda}$ and $X= Ae^{\sqrt{-\lambda}x} + Be^{-\sqrt{-\lambda}x}$ (provided $\lambda\ne 0$). So far $\lambda \in \mathbb{C}$.
Plugging into $X(0)=0$ and $X(l)=0$ we get \begin{align*} &A \qquad +B\qquad = 0,\\ &Ae^{\sqrt{-\lambda}l} + B e^{-\sqrt{-\lambda}l}=0 \end{align*} and this system has a non-trivial solution $(A,B)\ne 0$ if and only if its determinant is $0$: \begin{multline*} \left| \begin{matrix} 1 & 1\\ e^{\sqrt{-\lambda}l} & e^{-\sqrt{-\lambda}l}\end{matrix}\right|= e^{-\sqrt{-\lambda}l}-e^{\sqrt{-\lambda}l}=0\iff e^{2\sqrt{-\lambda}l}=1 \\ \iff 2\sqrt{-\lambda}l=2\pi ni \end{multline*} with $n=1,2,\ldots$. Here we excluded $n=0$ since $\lambda \ne 0$, and also $n=-1,-2,\ldots$ since both $n$ and $-n$ lead to the same $\lambda$ and $X$. The last equation is equivalent to (\ref{eq-4.1.9}). Then $k_{1,2}=\pm \frac{\pi n i}{l}$.
Meanwhile $B=-A$ anyway and we get $X=2Ai \sin (\frac{\pi n x}{l})$ i.e. (\ref{eq-4.1.10}) since the constant factor does not matter.
So far we have not covered $\lambda=0$. But then $k_{1,2}=0$ and $X=A+Bx$ and plugging into (\ref{eq-4.1.6}) we get $A=A+Bl=0 \implies A=B=0$ and $\lambda=0$ is not an eigenvalue.
After eigenvalue problem has been solved we plug $\lambda=\lambda_n$ into (\ref{eq-4.1.8}): \begin{equation} T''+ (\frac{c\pi n}{l})^2 T=0 \label{eq-4.1.12} \end{equation} which is also a 2-nd order linear ODE with constant coefficients.
Characteristic equation $k^2+ (\frac{c\pi n}{l})^2=0$ has solutions $k_{1,2}=\pm \frac{c\pi n i}{l}$ and therefore \begin{equation} T_n(t)=A_n \cos(\frac{c\pi nt}{l} ) + B_n \sin (\frac{c\pi nt}{l}) \label{eq-4.1.13} \end{equation} and finally we get a simple solution \begin{multline} u_n(x,t)= \underbrace{\bigl( A_n \cos(\frac{c\pi nt}{l} )+ B_n \sin (\frac{c\pi nt}{l} )\bigr)}_{=T_n(t)} \cdot \underbrace{\sin (\frac{\pi n x}{l})}_{=X_n(x)}\\ \text{with }\ n=1,2,\ldots \label{eq-4.1.14}\qquad\end{multline}
This simple solution (\ref{eq-4.1.14}) can be rewritten as \begin{equation*} u_n(x,t) =C_n \cos(\frac{c\pi nt}{l}+\phi_n)\sin (\frac{\pi n x}{l}) \end{equation*} and represents a standing wave

which one can decompose into a sum of running waves
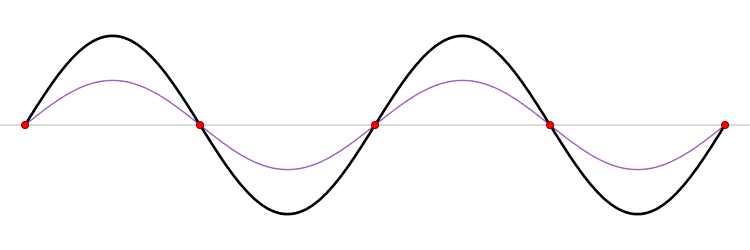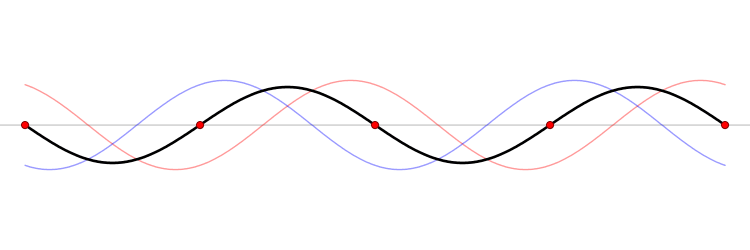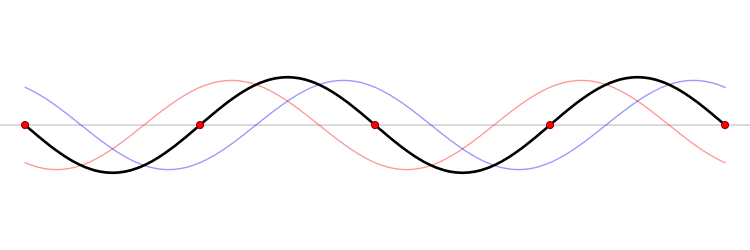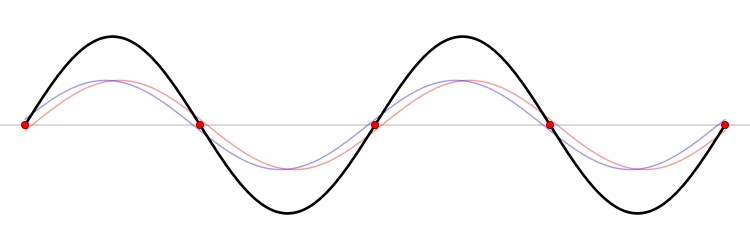
and the general discussion of standing waves could be found in wikipedia.
Points which do not move are called nodes and points with maximal amplitude are called antinodes.
The sum of solutions of (\ref{eq-4.1.1})-(\ref{eq-4.1.2}) is also a solution: \begin{equation} u(x,t)= \sum_{n=1}^\infty \bigl( A_n \cos(\frac{c\pi nt}{l} )+ B_n \sin (\frac{c\pi nt}{l} )\bigr) \cdot \sin (\frac{\pi n x}{l}). \label{eq-4.1.15} \end{equation} We have an important question to answer:
Have we covered all solutions of (\ref{eq-4.1.1})-(\ref{eq-4.1.2})? -- Yes, we did, but we need to justify it.
Plugging (\ref{eq-4.1.15}) into initial conditions (\ref{eq-4.1.3})1,2 (that is $u|_{t=0}=g(x)$ and $u_t|_{t=0}=h(x)$) we get respectively \begin{align} &\sum_{n=1}^\infty A_n \sin (\frac{\pi n x}{l})=g(x),\label{eq-4.1.16}\\ &\sum_{n=1}^\infty \frac{c\pi n}{l} B_n \sin (\frac{\pi n x}{l} )=h(x). \label{eq-4.1.17} \end{align}
How to find coefficients $A_n$ and $B_n$? Do they exist? Are they unique?
What we got are Fourier series (actually $\sin$-Fourier series). And we consider their theory in the several next sections.
More coming! Including multidimensional: