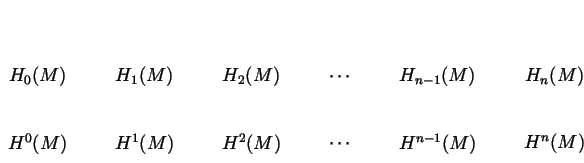Dreams on the (Co)Homology of Manifolds
The Context. Let 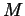 be an
be an 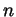 -dimensional manifold (a
topological space that locally looks like
-dimensional manifold (a
topological space that locally looks like
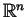 ) and let
) and let 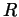 be a ring.
be a ring.
Dream 1
The following should be a list of spaces and their duals;
there ought to be no (co)homology beyond that list:
Dream 2
There should be an ``intersection pairing''
induced from the intersection pairing of submanifolds which ought to
satisfy
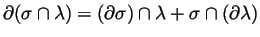
.
Dream 3
In particular, there should be a pairing
so with some further optimism,
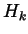
ought to be the same as
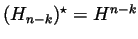
. (And why not call that ``Poincaré Duality''?)
Dream 4
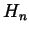
should be
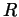
(and hence
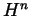
should be
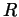
as
well).
Dream 5
There should be a ``cap product''
Dream 6
There should be a ``cup product''
and so
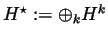
ought to be a ring!

Jules Henri Poincaré
Warning. Dreams are based on reality. Often,
distorted reality.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-03-31
![]() be an
be an ![]() -dimensional manifold (a
topological space that locally looks like
-dimensional manifold (a
topological space that locally looks like
![]() ) and let
) and let ![]() be a ring.
be a ring.