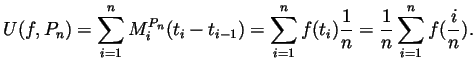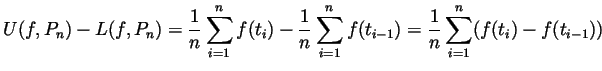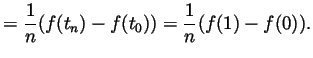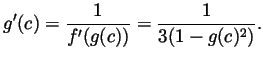Solution of Term Exam 3
Problem 1.
- Compute
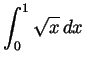 .
.
- Compute
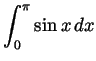 .
.
- For
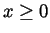 , compute
, compute
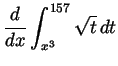 .
.
Solution. (Graded by Shay Fuchs)
- To use the second fundamental theorem of calculus we are looking for a
function
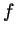 for which
for which
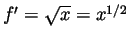 . The most obvious guess is
. The most obvious guess is
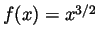 , but this is off by a factor of
, but this is off by a factor of 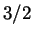 , for
, for
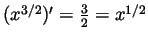 . So a good answer would be
. So a good answer would be
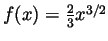 . Now
. Now
- Likewise choose
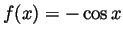 to get
to get
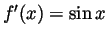 , and so using
the second fundamental theorem of calculus,
, and so using
the second fundamental theorem of calculus,
- Let
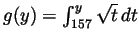 and let
and let 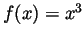 . Using the
first fundamental theorem of calculus,
. Using the
first fundamental theorem of calculus,
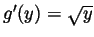 . So using the chain
rule,
. So using the chain
rule,
Problem 2.
- Perhaps using L'Hôpital's law, compute
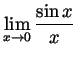 and
and
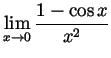 .
.
- Use these results to give educated guesses for the values of
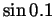 and
and 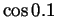 (no calculators, please).
(no calculators, please).
Solution. (Graded by Shay Fuchs)
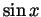 is differentiable at 0 and
is differentiable at 0 and 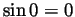 . So
(L'Hôpital's law also works and gives the same result).
. So
(L'Hôpital's law also works and gives the same result).
The second limit is of the form 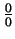 so we can use
L'Hôpital:
so we can use
L'Hôpital:
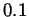 is close to 0, so
is close to 0, so
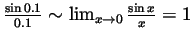 . Multiplying both
sides by
. Multiplying both
sides by 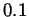 we get
we get
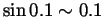 .
.
Likewise,
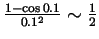 , so
, so
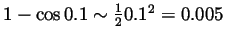 ,
so
,
so
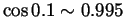 .
.
Problem 3.
- State the ``one partition for every
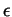 '' criterion of the
integrability of a bounded function
'' criterion of the
integrability of a bounded function 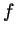 defined on an interval
defined on an interval
![$ [a,b]$](Solutionimg37.gif) .
.
- Let
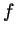 be an increasing function on
be an increasing function on ![$ [0,1]$](Solutionimg38.gif) and let
and let 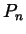 be the
partition defined by
be the
partition defined by 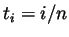 , for
, for
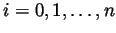 . Write simple formulas
for
. Write simple formulas
for 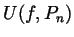 and for
and for 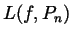 .
.
- Under the same conditions, write a very simple formula for
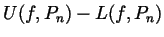 .
.
- Prove that an increasing function on
![$ [0,1]$](Solutionimg38.gif) is integrable.
is integrable.
Solution. (Graded by Derek Krepski)
- A bounded function
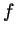 defined on an interval
defined on an interval ![$ [a,b]$](Solutionimg37.gif) is integrable
iff for every
is integrable
iff for every
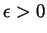 there is a partition
there is a partition 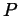 of
of ![$ [a,b]$](Solutionimg37.gif) for which
for which
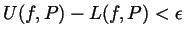 .
.
- As
 is increasing,
is increasing,
![$ m^{P_n}_i=\inf_{[t_{i-1},t_i]}f(x)=f(t_{i-1})$](Solutionimg48.gif) and
and
![$ M^{P_n}_i=\sup_{[t_{i-1},t_i]}f(x)=f(t_i)$](Solutionimg49.gif) . Thus
Likewise,
. Thus
Likewise,
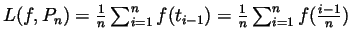 .
.
-
using telescopic summation this is
- Since
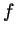 is increasing,
is increasing, 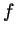 is bounded (with upper bound
is bounded (with upper bound 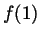 and
lower bound
and
lower bound 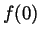 ). So using the criterion of part 1, to show that
). So using the criterion of part 1, to show that 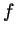 is
integrable it is enough to show that for every
is
integrable it is enough to show that for every
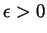 there is a
partition
there is a
partition 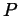 of
of ![$ [0,1]$](Solutionimg38.gif) for which
for which
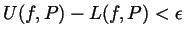 . Indeed, let
. Indeed, let
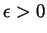 be given. Choose
be given. Choose 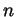 so big so that
so big so that
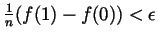 , and then the partition
, and then the partition 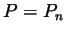 of before
satisfies
of before
satisfies
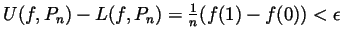 , as required.
, as required.
Problem 4.
- Show that the function
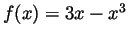 is monotone on the interval
is monotone on the interval
![$ [-1,1]$](Solutionimg61.gif) .
.
- Deduce that for every
![$ c\in[-2,2]$](Solutionimg62.gif) the equation
the equation 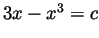 has a
unique solution
has a
unique solution 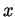 in the range
in the range
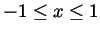 .
.
- For
![$ c\in[-2,2]$](Solutionimg62.gif) , let
, let 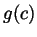 be the unique
be the unique 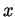 in the range
in the range
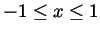 for which
for which 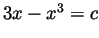 . Write a formula for
. Write a formula for 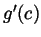 and
simplify it as much as you can. Your end result may still contain
and
simplify it as much as you can. Your end result may still contain 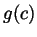 in
it, but not
in
it, but not 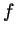 ,
, 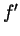 or
or 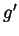 .
.
Solution. (Graded by Brian Pigott)
-
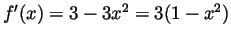 . On
. On 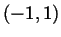 we know that
we know that 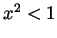 , so
, so
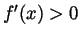 . So
. So 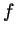 is increasing on
is increasing on ![$ [-1,1]$](Solutionimg61.gif) .
.
- By the theorem about the existence of inverses of monotone
functions,
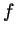 has an inverse on
has an inverse on ![$ [-1,1]$](Solutionimg61.gif) and it is defined on
and it is defined on
![$ [f(-1),f(1)]=[-2,2]$](Solutionimg74.gif) . This precisely means that for
. This precisely means that for
![$ c\in[-2,2]$](Solutionimg62.gif) the
equation
the
equation 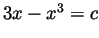 (which defines
(which defines 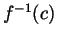 ) has a unique solution
with
) has a unique solution
with 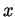 in the range
in the range
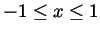 .
.
- By the theorem about the derivative of an inverse function,
The results. 67 students took the exam; the average
grade was 77.7 and the standard deviation was about 22.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-02-07
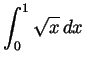 .
.
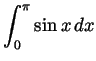 .
.
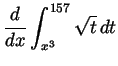 .
.
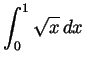 .
.
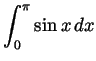 .
.
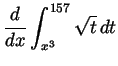 .
.
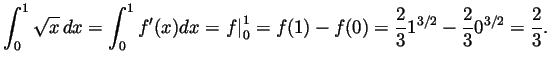
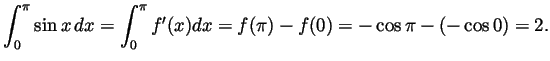
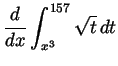
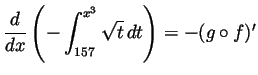
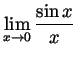 and
and
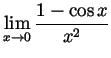 .
.
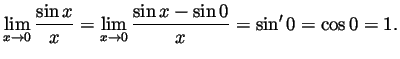
![]() so we can use
L'Hôpital:
so we can use
L'Hôpital:
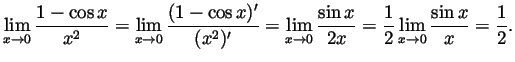
![]() , so
, so
![]() ,
so
,
so
![]() .
.