Homework Assignment 23
Assigned Tuesday March 29; due Friday April 8, 2PM,
at
SS 1071
Required reading. All of Spivak's Chapters 23
and 24.
To be handed in. From Spivak Chapter 24:
Problems 2 (odd parts), 5 (odd parts), 17, 23.
Recommended for extra practice. From Spivak
Chapter 24: 2 (even parts), 5 (even parts), 12, 15, 22, 24.
Just for fun 1. The series
is quite bizarre, as it converges uniformly to a continuous function
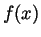 , yet that function
, yet that function 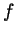 is so bumpy that it is not differentiable for
any
is so bumpy that it is not differentiable for
any 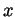 .
.
- Use theorems from class to show that
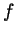 is indeed continuous and
that the converegence of the series is indeed uniform.
is indeed continuous and
that the converegence of the series is indeed uniform.
- Try to differentiate the series term by term and convince yourself
that after differentiation, there is no reason to expect the resulting
series to be convergent.
- Check numerically that
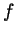 is not differentiable for any
is not differentiable for any 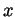 by
computing
by
computing
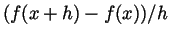 on your computer or calculator for very small
values of
on your computer or calculator for very small
values of 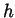 and for a number of different choices for
and for a number of different choices for 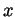 .
.
- Plot
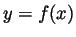 well enough to see that it is indeed very bumpy.
well enough to see that it is indeed very bumpy.
Just for fun 2. Another fun example for the use
of uniform convergence is the construction of a space-filling curve -- a
continuous function 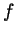 whose domain is the unit interval
whose domain is the unit interval 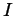 and whose
range is the entire unit square
and whose
range is the entire unit square 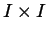 . (On first sight -- does
this seem possible??)
. (On first sight -- does
this seem possible??)
- This would be a function whose input is a single number and whose
output is a pair of numbers. Convince yourself that the words
``continuity'', ``convergence'' and ``uniform convergence'' can be
given a meaning in this context, and that they have similar properties as
in the case of ordinary functions.
- Do a web search to find (many!) pictures of space-filling curves (aka
``Peano curves'').
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-03-28
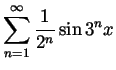
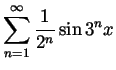
![]() whose domain is the unit interval
whose domain is the unit interval ![]() and whose
range is the entire unit square
and whose
range is the entire unit square ![]() . (On first sight -- does
this seem possible??)
. (On first sight -- does
this seem possible??)