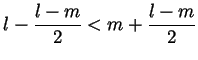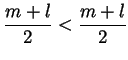Solution of Term Exam 1
Problem 1.
All that is known about the angle 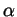 is that
is that
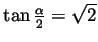 . Can you find
. Can you find
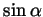 and
and
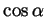 ? Explain your reasoning in full detail.
? Explain your reasoning in full detail.
Solution. (Graded by C.-N. (J.) Hung)
In class we wrote the formula
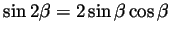 . Also
using
. Also
using
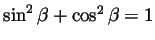 and taking
and taking
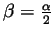 we get
we get
Dividing the numerator and denominator by
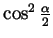 this
becomes
Likewise using
this
becomes
Likewise using
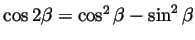 we get
we get
Problem 2.
- State the definition of the natural numbers.
- Prove that every natural number
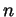 has the property that whenever
has the property that whenever
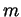 is natural, so is
is natural, so is 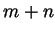 .
.
Solution. (Graded by V. Tipu)
- The set of natural numbers
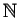 is the smallest set of numbers
for which
Alternatively, the set of natural numbers
is the smallest set of numbers
for which
Alternatively, the set of natural numbers
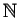 is the intersection of all
sets
is the intersection of all
sets 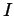 of numbers satisfying
of numbers satisfying
- Let
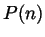 be the assertion ``whenever
be the assertion ``whenever 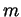 is natural, so is
is natural, so is 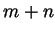 ''.
We prove
''.
We prove 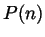 by induction on
by induction on 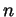 :
:
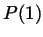 asserts that ``whenever
asserts that ``whenever 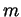 is natural, so is
is natural, so is 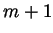 ''. This is
true by the second bullet in the definition of
''. This is
true by the second bullet in the definition of
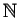 .
.
- Assume
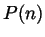 , that is, assume that whenever
, that is, assume that whenever 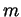 is natural, so is
is natural, so is
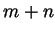 . Let
. Let 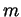 be a natural number. Then
be a natural number. Then
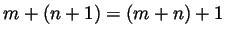 is a natural
number because by
is a natural
number because by 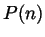 the number
the number 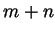 is natural and because adding one
to a natural number gives a natural number by the second bullet in the
definition of
is natural and because adding one
to a natural number gives a natural number by the second bullet in the
definition of
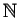 . So we have shown that whenever
. So we have shown that whenever 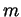 is natural so is
is natural so is
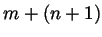 , and this is the assertion
, and this is the assertion 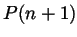 .
.
Problem 3.
Recall that a function 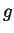 is called ``even'' if
is called ``even'' if
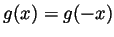 for all
for all
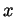 and ``odd'' if
and ``odd'' if
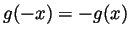 for all
for all 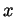 , and let
, and let 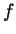 be some
arbitrary function.
be some
arbitrary function.
- Find an even function
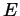 and an odd function
and an odd function 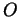 so that
so that 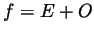 .
.
- Show that if
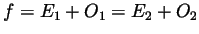 where
where 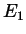 and
and 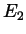 are even and
are even and
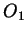 and
and 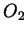 are odd, then
are odd, then 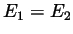 and
and 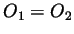 .
.
Solution. (Graded by C. Ivanescu)
- Set
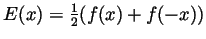 and
and
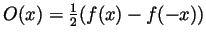 . Then
. Then
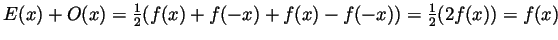 while
while
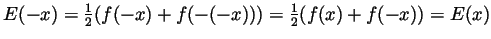 (so
(so 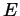 is even)
and
is even)
and
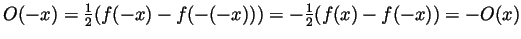 (so
(so 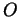 is
odd).
is
odd).
- Assume
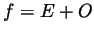 where
where 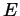 is even and
is even and 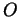 is odd. Then
So necessarily
is odd. Then
So necessarily
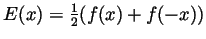 . Now if
. Now if
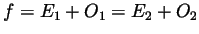 as above, then both
as above, then both 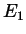 and
and 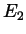 can play the role of
can play the role of 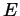 in this
argument, so they are both equal to
in this
argument, so they are both equal to
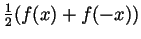 and in particular
they equal each other. Likewise,
and arguing like before,
and in particular
they equal each other. Likewise,
and arguing like before,
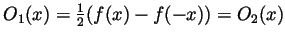 .
.
Problem 4.
Sketch, to the best of your understanding, the graph of the function
(What happens for 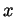 near 0? Near
near 0? Near 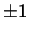 ? For large
? For large 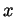 ? Is the graph
symmetric? Does it appear to have a peak somewhere?)
? Is the graph
symmetric? Does it appear to have a peak somewhere?)
Solution. (Graded by C. Ivanescu)
If 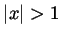 then
then 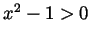 and so
and so
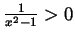 ; furthermore, the
larger
; furthermore, the
larger 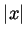 is (while
is (while 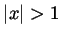 ), the larger
), the larger 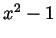 is and hence the
smaller
is and hence the
smaller
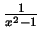 is. When
is. When 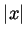 approaches
approaches 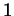 from above,
from above, 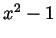 approaches 0 from above and hence
approaches 0 from above and hence
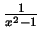 becomes larger and
larger. If
becomes larger and
larger. If 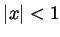 the
the 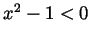 and so
and so
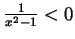 . When
. When 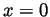 ,
, 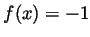 and when
and when 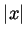 approaches
approaches 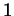 from below,
from below, 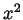 approaches
approaches 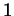 from below and
from below and 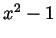 approaches 0 from
below, and so
approaches 0 from
below, and so
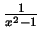 becomes more and more negative. In summary,
the graph looks something like:
becomes more and more negative. In summary,
the graph looks something like:
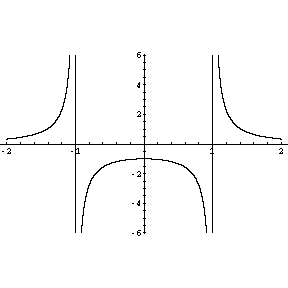
Problem 5.
- Suppose that
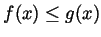 for all
for all 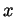 , and that the limits
, and that the limits
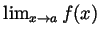 and
and
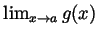 both exist. Prove that
both exist. Prove that
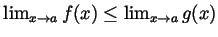 .
.
- Suppose that
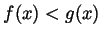 for all
for all 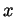 , and that the limits
, and that the limits
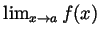 and
and
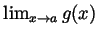 both exist. Is it always true
that
both exist. Is it always true
that
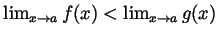 ? (If you think it's always true,
write a proof. If you think it isn't always true, provide a
counterexample).
? (If you think it's always true,
write a proof. If you think it isn't always true, provide a
counterexample).
Solution. (Graded by C.-N. (J.) Hung)
- Let
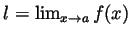 and
and
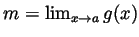 and assume by contradiction that
and assume by contradiction that 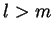 ; that is, that
; that is, that
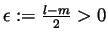 . Use the existence of the two limits to find
. Use the existence of the two limits to find
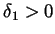 and
and
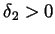 so that
and
Now choose some specific
so that
and
Now choose some specific 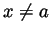 for which both
for which both
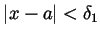 and
and
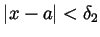 . But then
. But then
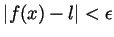 and so
and so
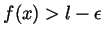 while
while
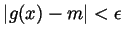 and so
and so
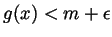 . Therefore remembering that
. Therefore remembering that
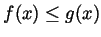 for all
for all 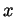 we get
or
or
which is a contradiction. Thus the assumption that
we get
or
or
which is a contradiction. Thus the assumption that 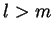 must be incorrect
and thus
must be incorrect
and thus 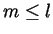 .
.
- Take
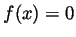 for all
for all 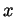 and
and 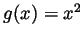 for all
for all 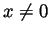 and
and
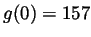 . Then
. Then 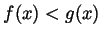 for all
for all 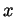 but
but
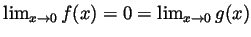 . So it isn't always true that if
. So it isn't always true that if
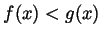 for all
for all 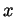 and the limits exist, then
and the limits exist, then
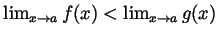 .
.
The results. 105 students took the exam; the average
grade was 67.19, the median was 70 and the standard deviation
was 21.12.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2004-10-18
![]() is that
is that
![]() . Can you find
. Can you find
![]() and
and
![]() ? Explain your reasoning in full detail.
? Explain your reasoning in full detail.
![]() . Also
using
. Also
using
![]() and taking
and taking
![]() we get
we get
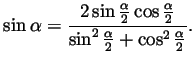
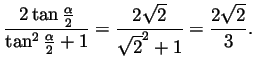
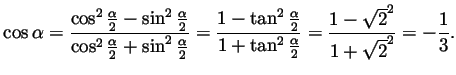
![]() is called ``even'' if
is called ``even'' if
![]() for all
for all
![]() and ``odd'' if
and ``odd'' if
![]() for all
for all ![]() , and let
, and let ![]() be some
arbitrary function.
be some
arbitrary function.
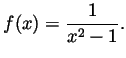
![]() then
then ![]() and so
and so
![]() ; furthermore, the
larger
; furthermore, the
larger ![]() is (while
is (while ![]() ), the larger
), the larger ![]() is and hence the
smaller
is and hence the
smaller
![]() is. When
is. When ![]() approaches
approaches ![]() from above,
from above, ![]() approaches 0 from above and hence
approaches 0 from above and hence
![]() becomes larger and
larger. If
becomes larger and
larger. If ![]() the
the ![]() and so
and so
![]() . When
. When ![]() ,
, ![]() and when
and when ![]() approaches
approaches ![]() from below,
from below, ![]() approaches
approaches ![]() from below and
from below and ![]() approaches 0 from
below, and so
approaches 0 from
below, and so
![]() becomes more and more negative. In summary,
the graph looks something like:
becomes more and more negative. In summary,
the graph looks something like: