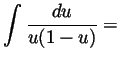
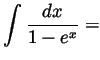
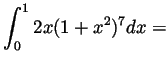
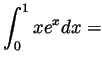
Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I:

(97)

Next: Solution of Term Exam 4 Previous: Class Notes for Thursday March 18, 2004

Term Exam 4

University of Toronto, March 22, 2004

This document in PDF: Exam.pdf

Solve the following 5 problems. Each is worth 20 points though in question 4 you may earn a 5 points bonus that brings the maximal possible total to 105/100. Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the tutors. You have an hour and 50 minutes.

Allowed Material: Any calculating device that is not capable of displaying text.

Good Luck!

Problem 1. Compute the following definite and indefinite integrals in elementary terms:

1. $$\int\frac{du}{u(1-u)}=$$
2. $$\int\frac{dx}{1-e^x}=$$
3. $$\int_0^1 2x(1+x^2)^7dx=$$
4. $$\int_0^1xe^xdx=$$

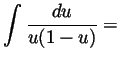
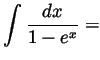
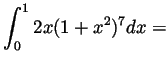
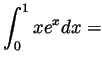
Problem 2. The ``unit ball'' $B$ in ${\mathbb{R}}^3$ is the result of revolving the domain $0\leq y\leq\sqrt{1-x^2}$ (for $-1\leq x\leq 1$) around the $x$ axis.

1. State the general ``Cosmopolitan Integral'' formula for the volume of a body obtained by revolving a domain bounded under the graph of a function $f$ around the $x$ axis.
2. Compute the volume of $B$.
3. State the general ``Cosmopolitan Integral'' formula for the surface area of a body obtained by revolving a domain bounded under the graph of a function $f$ around the $x$ axis.
4. Compute the surface area of $B$.

Problem 3. Let $\alpha$ be a real number which is not a positive integer or 0, let $f(x)=(1+x)^\alpha$ and let $n$ be a positive integer.

1. Compute the Taylor polynomial $P_{n,0,f}$ of degree $n$ for $f$ around 0.
2. Write the corresponding remainder term using one of the formulas discussed in class.
3. Determine (with proof) if there is an interval around 0 on which $$f(x)=\lim_{n\to\infty}P_{n,0,f}(x)$$.

Problem 4. Let $a_{n,m}$ be a ``sequence of sequences'' (an assignment of a real number $a_{n,m}$ to every pair $(n,m)$ of positive integers) and assume that $l_n$ is a sequence so that for every $n$ we have $\lim_{m\to\infty}a_{n,m}=l_n$. Further assume that $\lim_{n\to\infty}l_n=l$.

1. Show that for every positive integer $n$ there is a positive integer $m_n$
   so that $\vert a_{n,m_n}-l_n\vert<\vert l_n-l\vert+1/n$.
2. Show that $$\lim_{n\to\infty}a_{n,m_n} = l$$.
3. (5 points bonus, no partial credit) Is it always true that also $$\lim_{n\to\infty}a_{n,n}=l$$?

$${\begin{array}{cccccc} a_{1,1} & a_{1,2} & a_{1,3} & \ldots & \lo... ... \ddots & \vdots & \vdots \\ & & & & & \downarrow \\ & & & & & l \end{array}}$$

Problem 5.

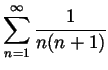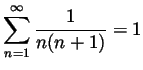1. Compute the first 5 partial sums of the series $$\sum_{n=1}^\infty\frac{1}{n(n+1)}$$.
2. Prove that $$\sum_{n=1}^\infty\frac{1}{n(n+1)}=1$$.

The generation of this document was assisted by L^ATEX2HTML.