| Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I: | (75) |
Next: Homework Assignment 19
Previous: Term Exam 3 |
Problem 1. In a very
condensed form, the definition of integration is as follows: For ![]() bounded on
bounded on ![]() and
and
![]() a partition of
a partition of
![]() set
set
![]() ,
,
![]() ,
,
![]() and
and
![]() . Then set
. Then set
![]() and
and
![]() . Finally, if
. Finally, if ![]() we say that
``
we say that
``![]() is integrable on
is integrable on ![]() '' and set
'' and set
![]() .
.
From this definition alone, without using anything proven in class
about integration, prove that the function ![]() given below is integrable on
given below is integrable on
![]() and compute its integral
and compute its integral
![]() :
:
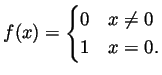
Solution. (Graded by Cristian Ivanescu) Let
![]() be an arbitrary partition of
be an arbitrary partition of ![]() . Then
for any
. Then
for any ![]() the infimum
the infimum
![]() is 0 and so
is 0 and so
![]() . Thus
. Thus
![]() .
At the same time, for any
.
At the same time, for any ![]() the supremum
the supremum
![]() is
is ![]() , and hence
, and hence
![]() and so
and so
![]() . Now let
. Now let
![]() be given and let
be given and let
![]() be
the partition
be
the partition
![]() . Then
. Then
![]() while
while ![]() and so
and so
![]() . Thus
. Thus
![]() . But this is true for any
. But this is true for any
![]() and we
already know that
and we
already know that
![]() . So it must be that
. So it must be that ![]() . Thus
. Thus
![]() and hence
and hence ![]() is integrable on
is integrable on ![]() and its integral
is
and its integral
is
![]() .
.
Problem 2. Prove that the function

Solution. (Graded by Julian C.-N. Hung) Differentiate
![]() using the first fundamental theorem of calculus. The first summand
yields
using the first fundamental theorem of calculus. The first summand
yields
![]() . The second summand is the first summand
pre-composed with the function
. The second summand is the first summand
pre-composed with the function
![]() . So by the chain rule,
the derivative of the second summand is
. So by the chain rule,
the derivative of the second summand is
![]() .
.
![]() is the sum of these two terms,
is the sum of these two terms,
![]() . Hence
. Hence ![]() is a constant.
is a constant.
Problem 3. In class we have proven that a
twice-differentiable function ![]() satisfying the equation
satisfying the equation ![]() is
determined by
is
determined by ![]() and
and ![]() . Use this fact and the known formulas for
the derivatives of
. Use this fact and the known formulas for
the derivatives of ![]() and
and ![]() to derive a formula for
to derive a formula for
![]() in terms of
in terms of
![]() ,
, ![]() ,
,
![]() and
and ![]() .
.
Solution. (Graded by Julian C.-N. Hung)
Let ![]() be a constant and consider the
functions
be a constant and consider the
functions
![]() and
and
![]() . Then
. Then
![]() and
and
![]() so both
so both ![]() and
and
![]() satisfy
satisfy ![]() . We also have
. We also have
![]() and
and
![]() . So by what we have proven in
class
. So by what we have proven in
class ![]() or
or
![]() .
.
Problem 4.
The function ![]() is defined by
is defined by ![]() .
.
Solution. (Graded by Vicentiu Tipu)
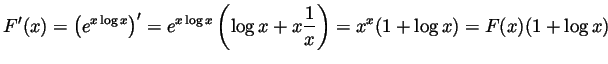 .
.
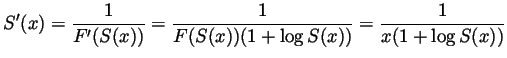 .
.
The results. 82 students took the exam; the average grade was 69.3, the median was 78 and the standard deviation was 26.76.