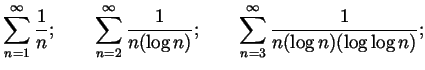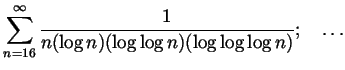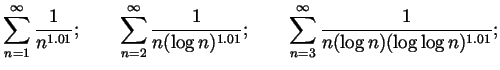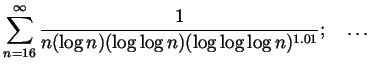| Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I: | (92) |
Next: Series
Previous: Class Notes for Thursday March 11, 2004 |
Required reading. All of Spivak Chapter 23. Then reread the Math 137 handouts ``How to Solve Problems'' and ``Guidelines to submitting problem sets''. Then read (and act upon) the following:
On Term Exam 4. It will take place, as scheduled, during the tutorials on Monday March 22nd. You will have an hour and 50 minutes to solve around 5 questions, with no choice questions. The material is everything covered in class until and including Tuesday March 15th, including everything in the relevant chapters (19 and its appendix, 20, 22, part of 23) of Spivak's book. The material in chapters 1-18 is not officially included, though, of course, what chance have you got answering questions about cosmopolitan integrals (say), if you aren't yet absolutely fluent with ordinary integrals?
Some of the questions may have a part in which you will be required to reproduce an example or a definition or a proof given in full in class or in the text. The class material is important; I put proofs on the blackboard because I really want you to understand them. Doing lots of exercises is great, but the most important exercises are the ones that are called ``theorems'' and are shown in class; that's precisely why they are shown in class!
Calculators will be allowed but will not be useful beyond emotional support; no devices that can display text will be allowed.
Important. You will take the exam in your usual tutorial classroom, except if the last non-zero digit of your student number is 5. in that case, if the digit to the left of the 5 is in the range 0-6, go to Vicentiu Tipu's tutorial at RW 142, and if it's in the range 7-9, go to Cristian Ivanescu's tutorial at UC 328.
Office hours. On Thursday March 18 I will hold my office hours between 1PM and 2PM, instead of the usual 12:30-1:30. Then on Friday March 19 I will hold special office hours at the Math Aid Centre (SS 1071), from 4:30PM until 6:30PM.
Preparing for Term Exam 3.
Remember. You really understand a mathematical definition / theorem / claim / lemma / anything only when you have fully internalized it and made it your own. Check if you can say to yourself one of the following:
It's worthwhile! Your grades will be higher, you will have gained more from this (and other) classes, and there is a lot of satisfaction and joy when you succeed. I internalized this sometime in my second year as an undergrad and it was the most important thing I learned that year.

Recommended for extra practice. From Spivak Chapter 23: 1, 5, 12, 20, 21, 21 as well as the following questions: