- Use
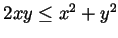 (why is this true?), with
(why is this true?), with
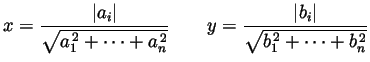
- Consider the expression
collect terms, and apply the result of Problem 1.
| Dror Bar-Natan: Classes: 2003-04: Math 157 - Analysis I: | (8) |
Next: Class Notes for Tuesday September 16, 2003
Previous: The 13 Postulates |
Required reading. All of Spivak Chapter 1.
To be handed in. From Spivak Chapter 1: 11 odd parts, 12 odd parts, 14, and also
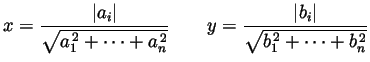
Recommended for extra practice. Spivak Chapter 1: 7, 15, 18, 20, 21, 22, 23.
Just for fun. Seen on the web, source unknown (though see http://www.mrc-cbu.cam.ac.uk/~matt.davis/Cmabrigde/):
Accdronig to a rscheearch at an Elingsh uinervtisy, it deosn't mttaer in waht oredr the ltteers in a wrod are, the olny iprmoatnt tihng is taht frist and lsat ltteer is at the rghit pclae. The rset can be a toatl mses and you can sitll raed it wouthit porbelm. Tihs is bcuseae we do not raed ervey lteter by it slef but the wrod as a wlohe.