Solution of the Final Exam
Problem 1. We say that a set 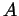 of real numbers is dense if for any open interval
of real numbers is dense if for any open interval 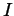 , the intersection
, the intersection 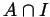 is
non-empty.
is
non-empty.
- Give an example of a dense set
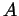 whose complement
whose complement
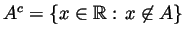 is also dense.
is also dense.
- Give an example of a non-dense set
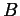 whose complement
whose complement
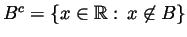 is also not dense.
is also not dense.
- Prove that if
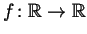 is an increasing function
(
is an increasing function
(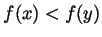 for
for 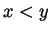 ) and if the range
) and if the range
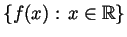 of
of 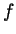 is
dense, then
is
dense, then 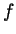 is continuous.
is continuous.
Solution.
- Take for example
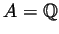 , the set of rational numbers. Then
, the set of rational numbers. Then 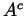 is
the set of irrational numbers. We've seen in class that between any two
(different) numbers (i.e., within any open interval) there is a rational
number and there is an irrational number. Hence both
is
the set of irrational numbers. We've seen in class that between any two
(different) numbers (i.e., within any open interval) there is a rational
number and there is an irrational number. Hence both 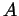 and
and 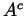 are
dense.
are
dense.
- Take for example
![$ B=[0,\infty]$](Solutionimg14.gif) , the set of non-negative
numbers. Then
, the set of non-negative
numbers. Then
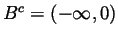 is the set of negative numbers. The
set
is the set of negative numbers. The
set 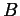 is not dense because, for example, it's intersection with the
interval
is not dense because, for example, it's intersection with the
interval 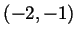 is empty. The set
is empty. The set 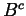 is not dense because, for
example, it's intersection with the interval
is not dense because, for
example, it's intersection with the interval 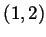 is empty.
is empty.
- We have to show that for every
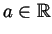 and for every
and for every
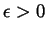 there is a
there is a 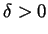 so that
so that
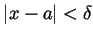 implies
implies
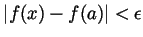 . So let
. So let
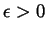 be given. By the density of
be given. By the density of
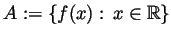 we know that we can find an element of
we know that we can find an element of 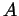 in
the interval
in
the interval
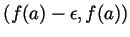 and another element of
and another element of 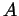 in the
interval
in the
interval
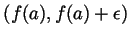 . That is, we can find
. That is, we can find 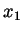 and
and 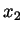 so that
so that
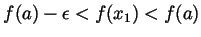 and
and
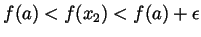 . It
follows from the monotonicity of
. It
follows from the monotonicity of 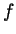 that
that 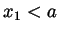 and that
and that 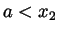 . Now
set
. Now
set
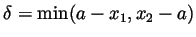 (this is a positive number because
(this is a positive number because
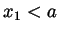 and
and 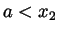 ). Finally if
). Finally if
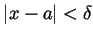 then
then 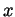 is in the
interval
is in the
interval
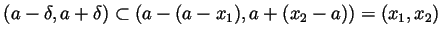 . By
the monotonicity of
. By
the monotonicity of 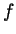 it follows that
it follows that 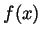 is in the interval
is in the interval
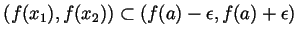 , and so
, and so
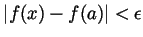 , as required.
, as required.
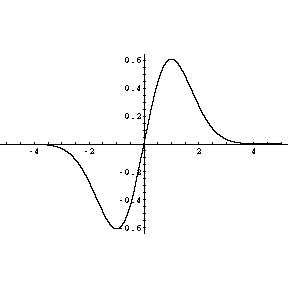
Problem 2. Sketch the graph of the function
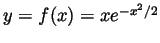 .
Make sure that your graph clearly indicates the following:
.
Make sure that your graph clearly indicates the following:
- The domain of definition of
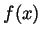 .
.
- The behaviour of
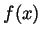 near the points where it is not defined (if
any) and as
near the points where it is not defined (if
any) and as
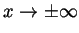 .
.
- The exact coordinates of the
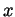 - and
- and
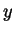 -intercepts and all minimas and maximas of
-intercepts and all minimas and maximas of 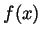 .
.
Solution. Our function is defined for all 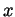 . As
. As 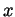 goes to
goes to 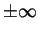 exponentials dominate polynomials, and so certainly
exponentials dominate polynomials, and so certainly
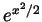 gets much bigger than
gets much bigger than 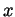 . So
. So
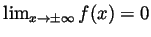 . Solving the equation
. Solving the equation
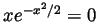 we see that the only intersection of the graph of
we see that the only intersection of the graph of 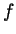 with the axes is
at
with the axes is
at 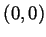 . We can compute
. We can compute
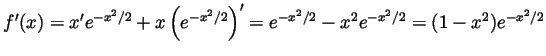 and
and
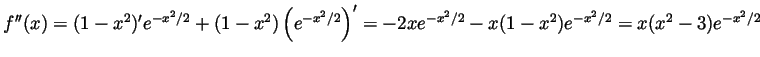 . Solving
. Solving 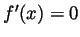 we see that the only critical points are when
we see that the only critical points are when 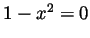 . That is, at
. That is, at
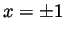 . As
. As
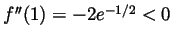 , the point
, the point
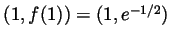 is a local max. As
is a local max. As
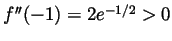 , the point
, the point
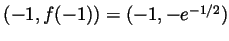 is a local min. As there are no other
critical points and the behaviour of
is a local min. As there are no other
critical points and the behaviour of 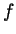 near the ends of its domain of
deifnition is mute (as determined before),
near the ends of its domain of
deifnition is mute (as determined before),
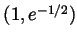 is actually a
global max and
is actually a
global max and
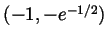 is actually a global min. Thus overall
the graph is:
is actually a global min. Thus overall
the graph is:
Problem and Solution 3. Compute the following derivative
and the following integrals:
- Using the fundamental theorem of calculus in the form
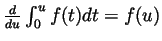 and the chain rule with
and the chain rule with 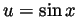 we
get
we
get
- We make the substitution
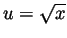 (and thus
(and thus 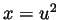 and
and
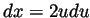 ) to compute
) to compute
- Integrating by parts twice we get
- We make the substitution
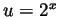 (and thus
(and thus 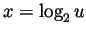 and
and
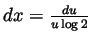 ) to compute
) to compute
- We use the factorization
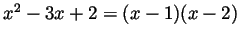 to get
to get
Problem 4. In solving this problem you are not
allowed to use any properties of the exponential function 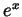 .
.
- Two differentiable functions,
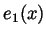 and
and 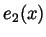 , defined over
the entire real line
, defined over
the entire real line
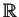 , are known to satisfy
, are known to satisfy
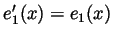 ,
,
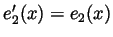 ,
, 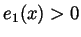 and
and 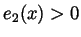 for all
for all
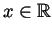 and also
and also
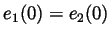 . Prove that
. Prove that 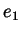 and
and 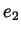 are the same. That is,
prove that
are the same. That is,
prove that
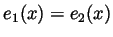 for all
for all
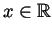 .
.
- A differentiable function
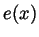 defined over the entire real
line
defined over the entire real
line
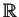 is known to satisfy
is known to satisfy
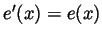 and
and 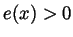 for all
for all
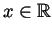 and also
and also 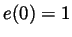 . Prove that
. Prove that
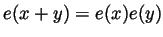 for all
for all
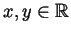 .
.
Solution.
- Set
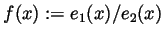 (this is well defined because
(this is well defined because 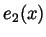 is
never 0) and compute
So
is
never 0) and compute
So 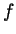 is a constant. But
is a constant. But
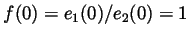 , so that constant is 1 and
, so that constant is 1 and
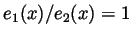 for all
for all 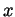 . This means that
. This means that 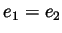 .
.
- Fix
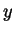 and set
and set
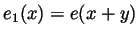 and
and
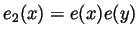 . Then
. Then
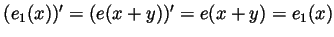 and
and
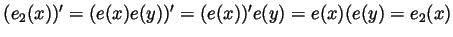 and
and
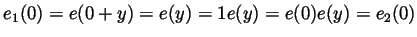 . All the other conditions of
the first part of this question are even easier to verify, and so the
conclusion of that part holds. Namely,
. All the other conditions of
the first part of this question are even easier to verify, and so the
conclusion of that part holds. Namely, 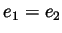 , which means
, which means
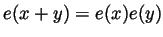 .
.
Problem 5. In solving this problem you are not
allowed to use any properties of the trigonometric functions.
- A twice-differentiable function
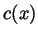 defined over the entire
real line
defined over the entire
real line
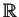 is known to satisfy
is known to satisfy
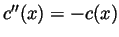 for all
for all
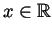 and also
and also
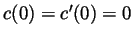 . Write out the degree
. Write out the degree 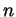 Taylor polynomial
Taylor polynomial
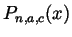 of
of 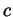 at
at 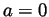 .
.
- Write a formula for the remainder term
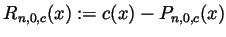 . (To keep the notation simple, you are
allowed to assume that
. (To keep the notation simple, you are
allowed to assume that 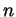 is even or even that
is even or even that 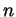 is divisible by 4).
is divisible by 4).
- Prove that
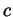 is the zero function:
is the zero function: 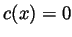 for all
for all
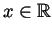 .
.
Solution.
- From
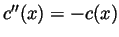 it is clear that
it is clear that
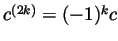 and that
and that
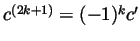 . So
. So
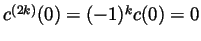 and
and
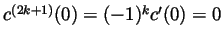 and hence all the coefficients of
and hence all the coefficients of
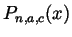 are 0. In other words,
are 0. In other words,
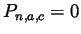 .
.
- If
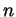 is divisible by
is divisible by 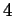 then
then
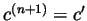 and so the remainder
formula says that for any
and so the remainder
formula says that for any 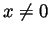 there is a
there is a 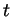 between 0 and
between 0 and 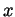 for
which
for
which
- Factorials grow faster then exponentials, so in the remainder
formula the denominator
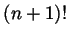 grows faster then the term
grows faster then the term
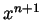 , while the numerator
, while the numerator 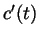 is bounded (by the theorem that a
continuous function on a closed interval is bounded). So the remainder goes
to 0 when
is bounded (by the theorem that a
continuous function on a closed interval is bounded). So the remainder goes
to 0 when 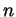 goes to
goes to 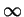 , and hence
, and hence
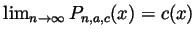 . But
. But
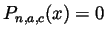 for all
for all 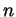 , so
necessarily
, so
necessarily 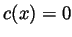 .
.
Remark 1. Two alternative forms of the remainder formula are
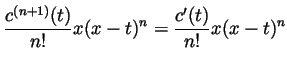
and
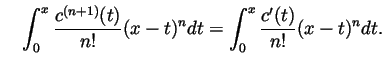
Either one of those could equaly well be used to solve part 3 of the
problem.
Remark 2. There is an alternative approach to the whole
problem; start with part 3 and go backwards. To do part 3, consider the
function
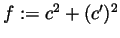 . We have
. We have
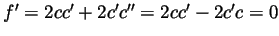 , so
, so 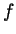 is a constant function. But
is a constant function. But
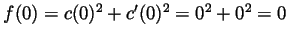 , so
, so 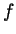 must be the 0 function. But
must be the 0 function. But 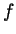 is a sum of squares, and the only way
a sum of squares can be 0 is if each summand is 0. So
is a sum of squares, and the only way
a sum of squares can be 0 is if each summand is 0. So 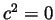 and
hence
and
hence 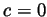 as required in part 3. But if
as required in part 3. But if 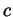 is the 0 function then
its Taylor polynomials are all 0 and the remainder terms are also all
0, solving parts 1 and 2 as well. This is not the solution I had in mind
when I wrote the problem, but people who solved the problem this way got
full credit.
is the 0 function then
its Taylor polynomials are all 0 and the remainder terms are also all
0, solving parts 1 and 2 as well. This is not the solution I had in mind
when I wrote the problem, but people who solved the problem this way got
full credit.
Problem 6. In solving this problem you are not allowed
to use the irrationality of 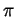 , but you are allowed, indeed advised,
to borrow a few lines from the proof of the irrationality of
, but you are allowed, indeed advised,
to borrow a few lines from the proof of the irrationality of 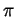 .
.
Is there a non-zero polynomial 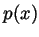 defined on the interval
defined on the interval ![$ [0,\pi]$](Solutionimg137.gif) and with values in the interval
and with values in the interval
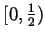 so that it and all of its
derivatives are integers at both the point 0 and the point
so that it and all of its
derivatives are integers at both the point 0 and the point 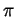 ? In
either case, prove your answer in detail.
? In
either case, prove your answer in detail.
Solution. There is no such polynomial. Had there been one,
we would have
but also, by repeated integration by parts (an even number of times, for
simplicity),
For any 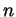 the first term in this formula involves only integers (as
the first term in this formula involves only integers (as
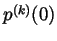 ,
,
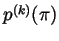 ,
, 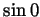 ,
, 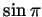 ,
, 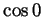 and
and 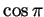 are all integers), and if
are all integers), and if 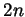 is
larger than the degree of
is
larger than the degree of 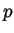 , the second term is 0. So
, the second term is 0. So
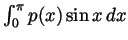 is an integer. But by the first formula it is
in
is an integer. But by the first formula it is
in 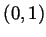 . That can't be.
. That can't be.
The results. 80 students took the exam; the average
grade was 69.33/120, the median was 71.5/120 and the standard deviation
was 26.51. The overall grade average for the course (of
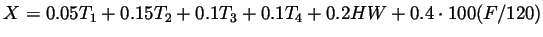 ) was
68.5, the median was 71.57 and the standard deviation was 18.64.
Finally, the transformation
) was
68.5, the median was 71.57 and the standard deviation was 18.64.
Finally, the transformation
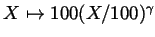 was applied to
the grades, with
was applied to
the grades, with
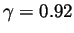 . This made the average grade 70.41, the
median 73.5 and the standard deviation 17.77. There were 30 A's (grades
higher or equal to 80) and 12 failures (grades below 50).
. This made the average grade 70.41, the
median 73.5 and the standard deviation 17.77. There were 30 A's (grades
higher or equal to 80) and 12 failures (grades below 50).
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2004-05-10
![]() of real numbers is dense if for any open interval
of real numbers is dense if for any open interval ![]() , the intersection
, the intersection ![]() is
non-empty.
is
non-empty.
![]() .
Make sure that your graph clearly indicates the following:
.
Make sure that your graph clearly indicates the following:
![]() . As
. As ![]() goes to
goes to ![]() exponentials dominate polynomials, and so certainly
exponentials dominate polynomials, and so certainly
![]() gets much bigger than
gets much bigger than ![]() . So
. So
![]() . Solving the equation
. Solving the equation
![]() we see that the only intersection of the graph of
we see that the only intersection of the graph of ![]() with the axes is
at
with the axes is
at ![]() . We can compute
. We can compute
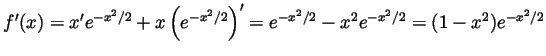 and
and
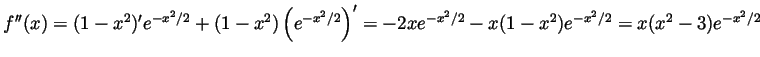 . Solving
. Solving ![]() we see that the only critical points are when
we see that the only critical points are when ![]() . That is, at
. That is, at
![]() . As
. As
![]() , the point
, the point
![]() is a local max. As
is a local max. As
![]() , the point
, the point
![]() is a local min. As there are no other
critical points and the behaviour of
is a local min. As there are no other
critical points and the behaviour of ![]() near the ends of its domain of
deifnition is mute (as determined before),
near the ends of its domain of
deifnition is mute (as determined before),
![]() is actually a
global max and
is actually a
global max and
![]() is actually a global min. Thus overall
the graph is:
is actually a global min. Thus overall
the graph is:

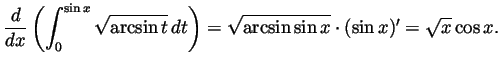
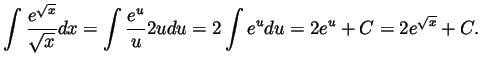
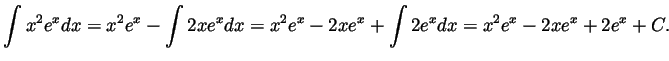
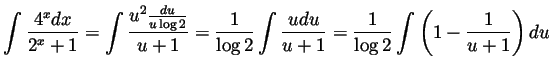
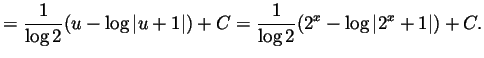
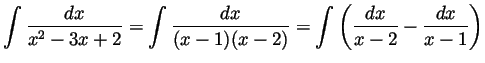
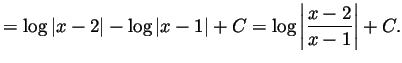
![]() .
.
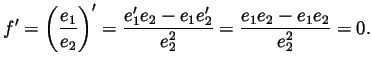
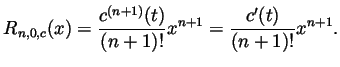
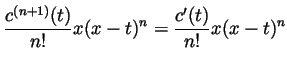 and
and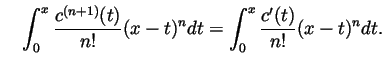
![]() . We have
. We have
![]() , so
, so ![]() is a constant function. But
is a constant function. But
![]() , so
, so ![]() must be the 0 function. But
must be the 0 function. But ![]() is a sum of squares, and the only way
a sum of squares can be 0 is if each summand is 0. So
is a sum of squares, and the only way
a sum of squares can be 0 is if each summand is 0. So ![]() and
hence
and
hence ![]() as required in part 3. But if
as required in part 3. But if ![]() is the 0 function then
its Taylor polynomials are all 0 and the remainder terms are also all
0, solving parts 1 and 2 as well. This is not the solution I had in mind
when I wrote the problem, but people who solved the problem this way got
full credit.
is the 0 function then
its Taylor polynomials are all 0 and the remainder terms are also all
0, solving parts 1 and 2 as well. This is not the solution I had in mind
when I wrote the problem, but people who solved the problem this way got
full credit.
![]() , but you are allowed, indeed advised,
to borrow a few lines from the proof of the irrationality of
, but you are allowed, indeed advised,
to borrow a few lines from the proof of the irrationality of ![]() .
.
![]() defined on the interval
defined on the interval ![]() and with values in the interval
and with values in the interval
![]() so that it and all of its
derivatives are integers at both the point 0 and the point
so that it and all of its
derivatives are integers at both the point 0 and the point ![]() ? In
either case, prove your answer in detail.
? In
either case, prove your answer in detail.
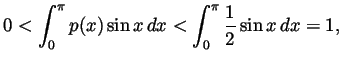
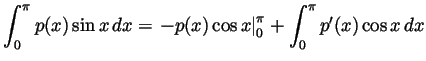
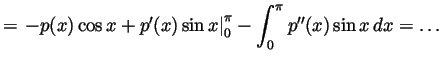
![]() ) was
68.5, the median was 71.57 and the standard deviation was 18.64.
Finally, the transformation
) was
68.5, the median was 71.57 and the standard deviation was 18.64.
Finally, the transformation
![]() was applied to
the grades, with
was applied to
the grades, with
![]() . This made the average grade 70.41, the
median 73.5 and the standard deviation 17.77. There were 30 A's (grades
higher or equal to 80) and 12 failures (grades below 50).
. This made the average grade 70.41, the
median 73.5 and the standard deviation 17.77. There were 30 A's (grades
higher or equal to 80) and 12 failures (grades below 50).