Solution of Term Exam 1
Problem 1.
- Prove directly from the postulates for the real numbers and from the
relevant definitions that if
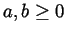 and
and 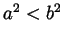 , then
, then 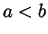 . If
you plan to use a formula such as
. If
you plan to use a formula such as
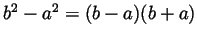 you don't need to
prove it, but of course you have to be very clear about how it is used.
you don't need to
prove it, but of course you have to be very clear about how it is used.
- Use induction to prove
that any integer
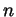 can be written in exactly one of the following
two forms:
can be written in exactly one of the following
two forms: 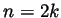 or
or 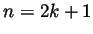 , where
, where 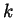 is also an integer.
is also an integer.
- Prove that there is no rational number
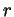 such that
such that 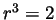 .
.
Solution.
- If
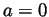 then
then 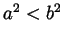 means that
means that 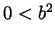 and therefore
and therefore 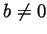 .
Along with
.
Along with 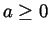 ,
, 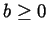 and P11, it follows that
and P11, it follows that 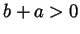 . If
. If 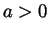 then again along with
then again along with 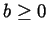 and P11 we get that
and P11 we get that 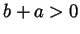 , so in either
case
, so in either
case 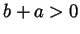 is assured. Now
is assured. Now
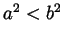 is by definition the same as
is by definition the same as 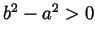 , and therefore
, and therefore
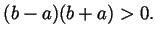 |
(1) |
Had 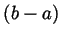 been negative, then
been negative, then 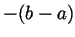 would have been positive and
by
would have been positive and
by 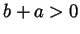 and P12 we'd have that
and P12 we'd have that
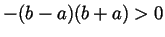 , contradicting
Equation (1). Hence
, contradicting
Equation (1). Hence 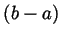 is positive, and this by
definition means that
is positive, and this by
definition means that 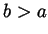 .
.
- First we show using induction that every natural number (positive
integer)
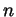 can be written in at least one of the forms
can be written in at least one of the forms 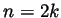 or
or
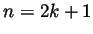 for an integer
for an integer 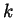 . Indeed, for
. Indeed, for 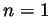 we write
we write
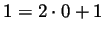 as required. Now if
as required. Now if 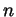 is of the form
is of the form 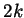 for an integer
for an integer 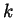 , then
, then
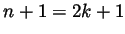 is of the second allowed form, and if
is of the second allowed form, and if 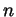 is of the form
is of the form
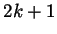 for some integer
for some integer 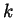 then
then
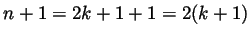 is of the first
allowed form, for
is of the first
allowed form, for 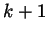 is also an integer. Therefore if
is also an integer. Therefore if 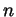 can be
written in either of the required forms then so is
can be
written in either of the required forms then so is 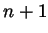 , and the
inductive proof is completed.
, and the
inductive proof is completed.
Let's deal with 0 and with the negative integers now. First,
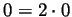 so 0 is of the form
so 0 is of the form 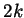 . Next, if
. Next, if 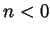 is an integer, then
is an integer, then 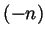 is a
positive integer and therefore
is a
positive integer and therefore 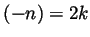 or
or 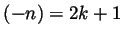 . In the former
case,
. In the former
case, 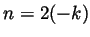 and we are done. In the latter case,
and we are done. In the latter case,
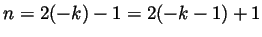 and again we are done.
and again we are done.
Finally, an integer cannot be of both forms at the same time, for if
we could write 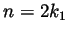 and
and 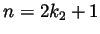 with integer
with integer 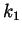 and
and 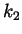 , then
we'd have that
, then
we'd have that
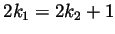 , which is
, which is
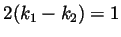 . But
. But 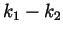 is an
integer and it is easy to show that
is an
integer and it is easy to show that 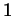 is not twice an integer.
is not twice an integer.
Having said all that, we can call the integers of the form 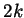 ``even''
and the integers of the form
``even''
and the integers of the form 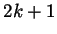 ``odd'', and then every integer is
either even or odd but never both.
``odd'', and then every integer is
either even or odd but never both.
- First,
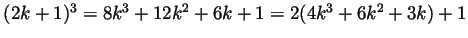 and hence if
and hence if 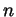 is odd then so is
is odd then so is 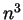 . Therefore if
. Therefore if 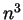 is even then so is
is even then so is 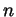 . Now
assume by contradiction that there is some rational number
. Now
assume by contradiction that there is some rational number 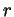 with
with 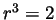 and write
and write 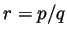 where
where 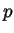 and
and 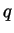 are integers and
are integers and 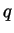 is the least
positive integer for which it is possible to present
is the least
positive integer for which it is possible to present 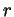 in this form. Now
in this form. Now
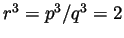 hence
hence 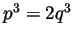 is even hence
is even hence 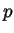 is even hence we can
find an integer
is even hence we can
find an integer 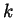 with
with 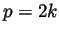 . But then
. But then 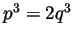 becomes
becomes 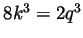 and hence
and hence
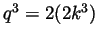 so
so 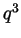 is even and hence so is
is even and hence so is 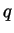 , so
, so 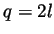 for
some positive
for
some positive 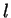 (which of course is smaller than
(which of course is smaller than 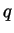 itself). But now
itself). But now
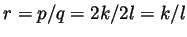 contradicting the minimality of
contradicting the minimality of 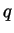 . Therefore there is
no rational number
. Therefore there is
no rational number 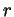 with
with 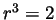 .
.
Problem 2.
- Suppose
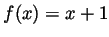 . Are there any functions
. Are there any functions 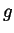 such that
such that
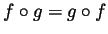 ?
?
- Suppose that
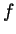 is a constant function. For which functions
is a constant function. For which functions 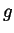 does
does
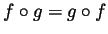 ?
?
- Suppose that
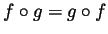 for all functions
for all functions 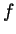 . Show
that
. Show
that 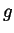 is the identity function
is the identity function 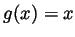 .
.
Solution.
- Yes. For example, the identity function
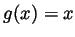 has this property.
has this property.
- Suppose
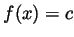 for all
for all 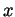 . Then
. Then
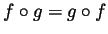 if and only if
if and only if
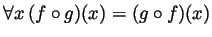 iff
iff
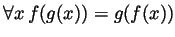 iff
iff
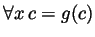 iff
iff 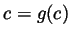 . So
. So 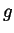 satisfies
satisfies
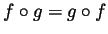 iff
iff
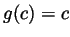 .
.
- If
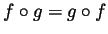 for all functions
for all functions 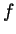 then in particular
then in particular
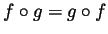 for all constant functions
for all constant functions 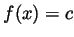 . But then by the
previous part for all constant
. But then by the
previous part for all constant 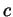 we have
we have 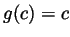 and this precisely
means that
and this precisely
means that 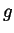 is the identity function
is the identity function 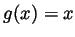 .
.
Problem 3. Sketch, to the best of your understanding, the
graph of the function
(What happens for 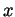 near 0? For large
near 0? For large 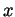 ? Where does the graph lie
relative to the graph of the function
? Where does the graph lie
relative to the graph of the function 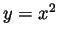 ?)
?)
Solution. The first graph below shows 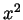 (above the
(above the
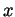 axis) and
axis) and 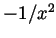 (below the
(below the 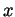 axis. The second shows the sum of the
two, the desired function
axis. The second shows the sum of the
two, the desired function 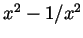 :
:
For 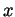 near 0 our function goes
to
near 0 our function goes
to 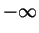 , for large
, for large 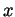 it goes to
it goes to 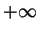 . It is always below
. It is always below 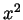 but for large
but for large 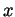 it is very near
it is very near 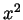 .
.
Problem 4. Write the definition of
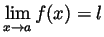 and give examples to show that the
following definitions of
and give examples to show that the
following definitions of
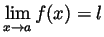 do not
agree with the standard one:
do not
agree with the standard one:
- For all
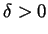 there is an
there is an
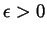 such that if
such that if
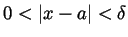 , then
, then
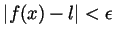 .
.
- For all
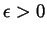 there is a
there is a 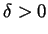 such that if
such that if
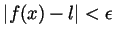 , then
, then
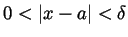 .
.
Solution. The definition is: For every
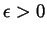 there is a
there is a 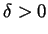 so that whenever
so that whenever
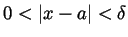 we have that
we have that
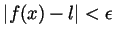 . The required examples:
. The required examples:
- This is satisfied whenever
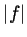 is bounded and regardless of its
limit. Indeed, choose
is bounded and regardless of its
limit. Indeed, choose 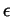 bigger than
bigger than 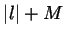 where
where 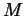 is a bound
on
is a bound
on 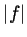 , and
, and
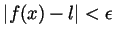 is always true.
is always true.
- According to this definition, for example,
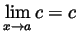 is false, and hence it cannot be equivalent to the standard
definition. Indeed, in this case
is false, and hence it cannot be equivalent to the standard
definition. Indeed, in this case
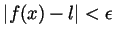 means
means
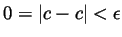 .
This imposes no condition on
.
This imposes no condition on 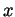 , so
, so 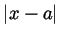 need not be smaller than
need not be smaller than
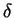 .
.
Problem 5. Suppose that 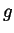 is continuous at 0 and
is continuous at 0 and
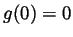 and that
and that
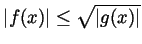 for all
for all 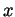 . Show that
. Show that 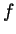 is
continuous at 0.
is
continuous at 0.
Solution. At 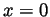 the inequality
the inequality
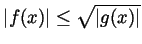 reads
reads
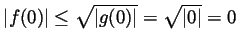 , and hence
, and hence 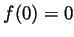 . We claim
that
. We claim
that
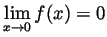 and hence that
and hence that 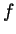 is continuous at
0. Indeed let
is continuous at
0. Indeed let
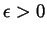 be given. Then
be given. Then
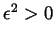 and by the
continuity of
and by the
continuity of 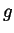 at 0 we can find a
at 0 we can find a 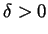 so that whenever
so that whenever
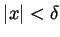 we have that
we have that
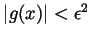 . But then if
. But then if
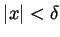 then
then
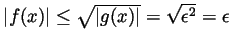 and the definition of
and the definition of
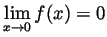 is satisfied.
is satisfied.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2002-10-23
![]() so 0 is of the form
so 0 is of the form ![]() . Next, if
. Next, if ![]() is an integer, then
is an integer, then ![]() is a
positive integer and therefore
is a
positive integer and therefore ![]() or
or ![]() . In the former
case,
. In the former
case, ![]() and we are done. In the latter case,
and we are done. In the latter case,
![]() and again we are done.
and again we are done.
![]() and
and ![]() with integer
with integer ![]() and
and ![]() , then
we'd have that
, then
we'd have that
![]() , which is
, which is
![]() . But
. But ![]() is an
integer and it is easy to show that
is an
integer and it is easy to show that ![]() is not twice an integer.
is not twice an integer.
![]() ``even''
and the integers of the form
``even''
and the integers of the form ![]() ``odd'', and then every integer is
either even or odd but never both.
``odd'', and then every integer is
either even or odd but never both.
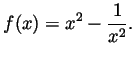
![]() (above the
(above the
![]() axis) and
axis) and ![]() (below the
(below the ![]() axis. The second shows the sum of the
two, the desired function
axis. The second shows the sum of the
two, the desired function ![]() :
:

![]() near 0 our function goes
to
near 0 our function goes
to ![]() , for large
, for large ![]() it goes to
it goes to ![]() . It is always below
. It is always below ![]() but for large
but for large ![]() it is very near
it is very near ![]() .
.
![]() and give examples to show that the
following definitions of
and give examples to show that the
following definitions of
![]() do not
agree with the standard one:
do not
agree with the standard one:
![]() there is a
there is a ![]() so that whenever
so that whenever
![]() we have that
we have that
![]() . The required examples:
. The required examples:
![]() is continuous at 0 and
is continuous at 0 and
![]() and that
and that
![]() for all
for all ![]() . Show that
. Show that ![]() is
continuous at 0.
is
continuous at 0.
![]() the inequality
the inequality
![]() reads
reads
![]() , and hence
, and hence ![]() . We claim
that
. We claim
that
![]() and hence that
and hence that ![]() is continuous at
0. Indeed let
is continuous at
0. Indeed let
![]() be given. Then
be given. Then
![]() and by the
continuity of
and by the
continuity of ![]() at 0 we can find a
at 0 we can find a ![]() so that whenever
so that whenever
![]() we have that
we have that
![]() . But then if
. But then if
![]() then
then
![]() and the definition of
and the definition of
![]() is satisfied.
is satisfied.