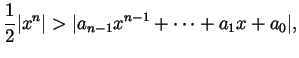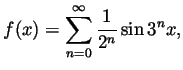Homework Assignment 8
Assigned Tuesday October 29; due Friday November 8, 2PM at SS 1071
All of Spivak Chapter 9.
From Spivak Chapter 9: 1, 9, 15, 23.
From Spivak Chapter 9: 8, 11, 21, 28.
Also, let 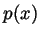 be the polynomial
be the polynomial
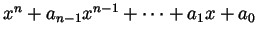 . Now that we know that for
. Now that we know that for
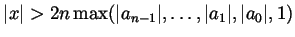 we have that
we have that
complete the proof of the following
Theorem.
- If
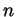 is odd then the equation
is odd then the equation 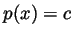 has a root for any value of
has a root for any value of
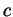 .
.
- If
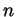 is even then there is some constant
is even then there is some constant 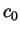 so that the equation
so that the equation
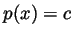 has no roots for
has no roots for 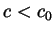 , has at least one root for
, has at least one root for 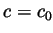 and at
least two roots for
and at
least two roots for 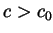 .
.
Write a computer program that will allow you to
draw the graph of the function
and will allow you to zoom on that graph through various small
``windows''. Use your program to convince yourself that 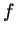 is
everywhere continuous but nowhere differentiable. The best plots will
be posted on this web site! (Send pictures along with window
coordinates by email to
drorbn@math.toronto.edu).
is
everywhere continuous but nowhere differentiable. The best plots will
be posted on this web site! (Send pictures along with window
coordinates by email to
drorbn@math.toronto.edu).
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2002-10-28
![]() be the polynomial
be the polynomial
![]() . Now that we know that for
. Now that we know that for
![]() we have that
we have that