| Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I: | (286) |
Next: Class Home
Previous: Final Exam |
Problem 1. Let ![]() and
and ![]() denote functions defined on
some set
denote functions defined on
some set ![]() .
.
Solution.
Problem 2. Sketch the graph of the function
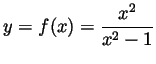 . Make sure that your graph
clearly
indicates the following:
. Make sure that your graph
clearly
indicates the following:
Solution. ![]() is defined for
is defined for
![]() , and the
following limits are easily computed:
, and the
following limits are easily computed:
![]() ,
,
![]() and
and
![]() . The only solution for
. The only solution for
![]() is
is ![]() , hence the only intersection of the graph of
, hence the only intersection of the graph of ![]() with
the axes is at
with
the axes is at ![]() . Other than at
. Other than at ![]() , the numerator of
, the numerator of ![]() is always
positive, hence the sign of the function is determined by the sign of the
denominator
is always
positive, hence the sign of the function is determined by the sign of the
denominator ![]() . Thus
. Thus
![]() for
for ![]() and
and ![]() for
for
![]() . Finally
. Finally
![]() and thus
and thus
![]() is positive and
is positive and ![]() is increasing (locally) for
is increasing (locally) for ![]() and
and ![]() is
negative and
is
negative and ![]() is decreasing (locally) for
is decreasing (locally) for ![]() .
Thus overall the graph is:
.
Thus overall the graph is:
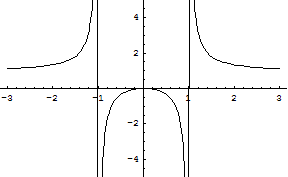
Problem 3. Compute the following integrals:
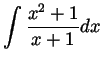
Solution. By long division of polynomials,
![]() . Thus we can rewrite our integral as a sum of two
terms as follows
. Thus we can rewrite our integral as a sum of two
terms as follows
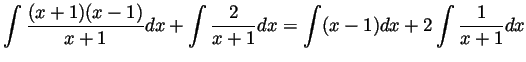
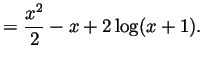
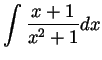
Solution. Again we rewrite the integral as a sum of two
terms. On the first we perform the substitution ![]() ; the second is
elementary:
; the second is
elementary:
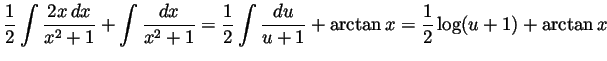
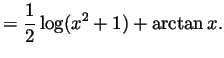
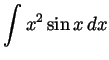
Solution. We integrate by parts twice, as follows:
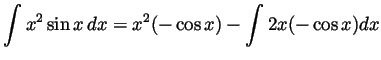
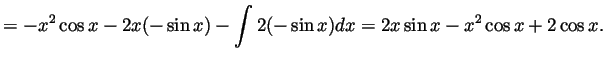
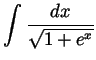
Solution. Set
![]() and then
and then ![]() and
and
![]() and so
and so
![]() and
and
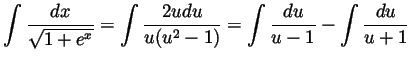
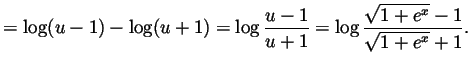
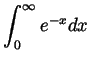
Solution.
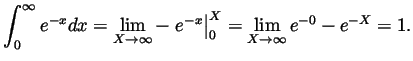
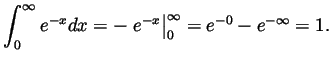
Problem 4. Agents of the
CSIS have secretly developed a
function ![]() that has the following properties:
that has the following properties:
Solution.
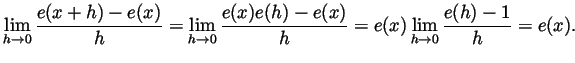
Problem 5.
Solution.
Problem 6. Prove that the complex function
![]() is everywhere continuous but nowhere differentiable.
is everywhere continuous but nowhere differentiable.
Solution. The key point is that
![]() for
every complex number
for
every complex number ![]() . Let
. Let
![]() and set
and set
![]() .
Now if
.
Now if
![]() then
then
![]() . This
proves the continuity of
. This
proves the continuity of
![]() . Let us check if this function
is differentiable:
. Let us check if this function
is differentiable:
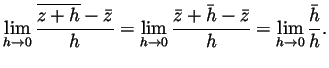
The results. 76 students took the exam; the average
grade was 72.66/120, the median was 71.5/120 and the standard deviation
was 25.5. The overall grade average for the course (of
![]() ) was
66.92, the median was 64.9 and the standard deviation was 17.16.
Finally, the transformation
) was
66.92, the median was 64.9 and the standard deviation was 17.16.
Finally, the transformation
![]() was applied to
the grades, with
was applied to
the grades, with
![]() . This made the average grade 71.55, the
median 70 and the standard deviation 15.31. There were 25 A's (grades
above 80) and 5 failures (grades below 50).
. This made the average grade 71.55, the
median 70 and the standard deviation 15.31. There were 25 A's (grades
above 80) and 5 failures (grades below 50).