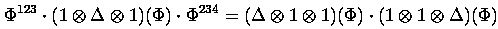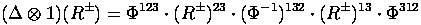More details: Finite type invariants are invariants of knots that can be regarded, in a natural sense, as polynomials on the space of all knots. It is a pretty powerful bunch of invariants, though they are better liked for their beauty rather than their power. By the fundamental theorem, they are classified by certain nice combinatorial objects called chord diagrams (close relatives of the Feynman diagrams of quantum field theory), modulo certain nice relations that are deeply related to Lie algebras. In the first part of the course we will talk about knots, knot invariants, finite type knot invariants, chord diagrams and their basic algebraic properties, and about the relationship with Lie algebras. We will then choose between either one of two of the approaches to proving the fundamental theorem, which, as we shall see, is equivalent to the construction of a universal finite type invariant:
- The mystical/physical/geometrical approach:
- One looks at the Feynman diagram expansion of a certain quantum field
theory, and hoopla, we get a universal finite type invariant! Or else,
one studies some strange systems of integrals over certain
configuration spaces, or some odd "chopstick counting"
problems, and hoopla again.
Key words and phrases: perturbation theory, Feynman diagrams, configuration spaces, compactification, differential forms and Stokes' theorem, degrees and general position, etc.
Some key formulas: 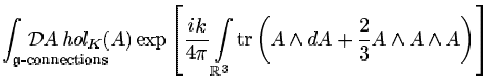
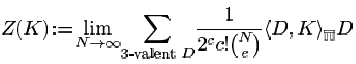
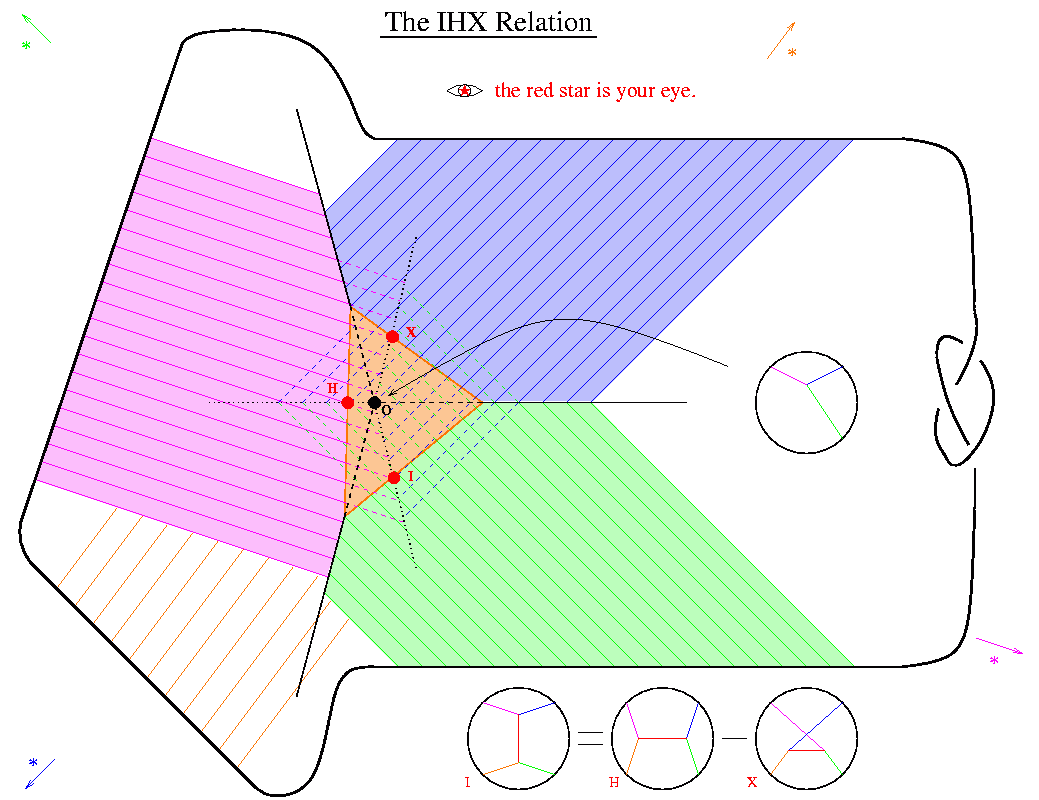
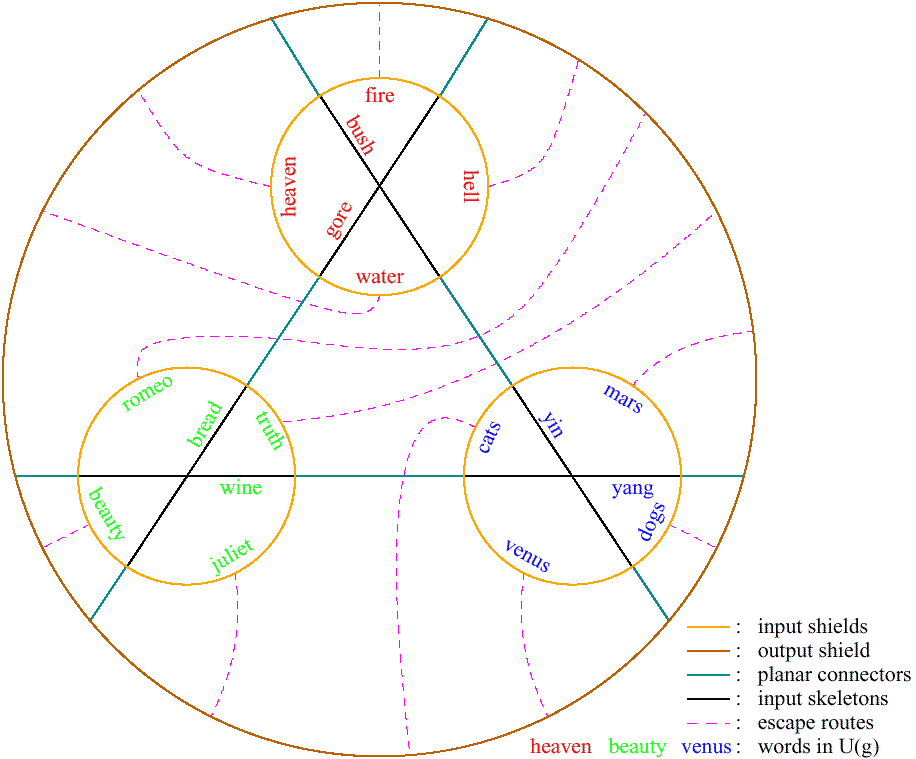
A key picture: