From Astrology to Topology via Feynman Diagrams and Lie Algebras

Dror Bar-Natan

brief notes for lectures given in Srni, January 1999
published at Rendiconti Del Circolo Matematico Di Palermo Serie II Suppl. 63 (2000) 11-16

Date: November 25, 1999.

Institute of Mathematics
The Hebrew University
Giv'at-Ram, Jerusalem 91904
Israel

drorbn@math.toronto.edu

The lecture announcements are at http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/.
This document is http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/notes.html.
A PostScript version is at http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/notes.ps.
The TeX source is at http://www.math.toronto.edu/~drorbn/Talks/Srni-9901/notes.uu (see directions there).

Contents

• First lecture
• Second lecture
• Third lecture
• Bibliography
• About this document ...

First lecture

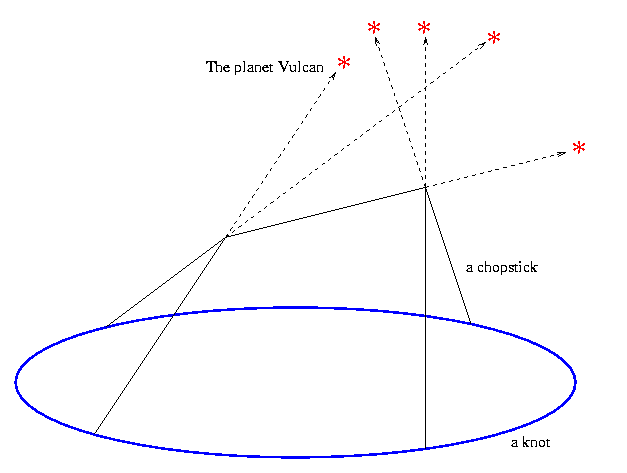
We started by viewing some pictures of Stonehenge ,

as well as a picture from an advertisement campaign of Andersen Consulting, a company totally unrelated to my Århus friend Jørgen Ellegaard Andersen:

Are your stars in optimal alignment?

These stellar images motivated us to study stellar coincidences. We therefore picked a knot, given as a specific embedding of $S^1$ in ${\mathbb{R}}^3$, and counted (with signs) the number of ``Stonehenge-inspired chopstick towers'' that can be built upon it; namely, the number of delicate arrangements of chopsticks whose ends are lying on the knot or are supporting each other in trivalent corners joining three chopsticks each, so that each chopstick is pointing at a different pre chosen point in heaven that has a high mythical meaning. One example of such ``Stonehenge-inspired chopstick tower'' is below:

a Stonehenge-inspired chopstick tower.

These ``chopstick counts'' can be all incorporated together to produce a single ``generating function'', by setting

$$Z:K\mapsto Z(K) = \sum_D \frac{1}{2^c c!}<D,K>_S\cdot D,$$

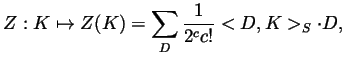
where $<D,K>_S$ denotes the ``Stonehenge pairing'' of a diagram $D$ (that is made of $c$ chopsticks) with a given knot embedding $K$; that is, the (signed) number of ways a chopstick tower whose underlying combinatorics is $D$ can be placed upon the specific embedding $K$. The whole sum $Z(K)$ should be interpreted as living in the vector space of infinite formal linear combinations of possible diagrams $D$.

We then argued that when the target space of $Z(K)$ is divided by appropriate relations (the AS, IHX, and STU relations), and $Z(K)$ is modified in a minor way to correct for problems related to framings of $K$, then the new $Z(K)$ is an invariant of knots valued in some space $A$ of ``diagrams modulo relations''.

The idea of our argument was to deform $K$ while carefully tracing what happens to a chopstick tower built upon it. Generically, such towers simply move along with the knot, while continuously deforming. Such continuous deformations do not alter the combinatorics underlying the tower, and hence $Z(K)$ does not change. But occasionally a catastrophe occurs, and a whole tower completely disappears or is newly created. We studied the times when such catastrophes occur, and found that towers always appear or disappear in pairs with opposite sign (with $Z(K)$ remaining fixed) or in groups of three which are IHX- or STU-related. Hence in the quotient space by IHX and STU, the space $A$, we see that $Z(K)$ remains invariant.

Literature guide: $Z(K)$ was first defined (using different terminology) by Dylan Thurston in his Harvard undergraduate thesis [Th]. His thesis was a continuation and completion of the work started by Bott and Taubes in [BT] (see also [Bo]). The more standard language in which $Z(K)$ is described is the language of de-Rham forms on compactified configuration spaces; this is the language used in most of [Th], in [BT] and [Bo], and in the later article by Altschuler and Freidel [AF]. (The two languages amount to two ways of computing the degree of a map; one by counting inverse images of a generic point, and one by integrating the pull back of a top form). We note that significant further progress along these lines was made by Yang [Ya] and by Poirier [Po1,Po2].

After discussing $Z(K)$, we moved on to talk about finite type invariants of knots and links. The idea was to define ``a derivative'' of a knot invariant $V$ to be a difference of its values on two neighboring knots (knots that differ in only one crossing), and then to define higher order derivatives as iterated differences. Once derivatives are around, one can talk about ``polynomials'' - invariants whose high derivatives vanish. In the case of knots, such invariants are called ``finite type invariants'' or ``Vassiliev invariants''.

Literature guide: Vassiliev invariants were first defined by Goussarov [Go1,Go2] and Vassiliev [Va1,Va2]. A definition in the spirit of the above paragraph and much further information can be found in [B-N4], and an even closer relationship between Vassiliev invariants and polynomials is in [B-N6]. Many classical knot and link invariants are Vassiliev invariants; see [Go1,B-N2,BL,B-N4,Bi,B-N5]. An extensive bibliography of Vassiliev invariants is available on the Web.

Second lecture

We started by completing the discussion of finite type invariants of knots along the lines of [B-N4], introducing chord diagrams, weight systems and the 4T relation, the STU relation (which is equivalent to the 4T relation), and the notion of ``a universal Vassiliev invariant'' (of which $Z(K)$ is an example).

We then went on trying to sooth the skeptics into quiet submission by showing how the mystic construction of $Z(K)$ is a direct descendent of the Chern-Simons quantum field theory (whose relation to knot theory was first discovered by Witten [Wi]). We started by recalling perturbation theory and Feynman diagrams. This is of course a classical subject, and there is much written about it in many places. Two specific places that use notation that I like (naturally) are [B-N1] and [Å1, Appendix]. The latter source uses the same notation as in the lecture. Anyway, we then went and briefly mentioned the specific way Chern-Simons theory relates to knot theory via Feynman diagrams. More details are in [B-N1] and in [BS, Section 3]. It can be shown that the integrals that arise in this way from Feynman diagrams are the same as the Bott-Taubes configuration space integrals [BT], and that those are the same as our construction of $Z(K)$ (see [Th]).

Third lecture

This lecture was devoted to the Århus integral of Bar-Natan, Garoufalidis, Rozansky, and Thurston -- an alternative construction of the LMO invariant of 3-manifolds, in the case of rational homology spheres.

The basic idea was to adopt a ``monkey's view of algebra''. We argued that from a monkey's perspective, the space $A$ can be viewed as if it is the universal enveloping algebra of some Lie algebra $g$, and therefore by the Poincare-Birkhoff-Witt it should be isomorphic to some space $B$ of uni-trivalent diagrams modulo the AS and IHX relations, which is the monkey's version of the symmetric algebra $S(g)$ of $g$. Now people can think of $S(g)$ as the algebra of polynomials over $g^\star$, and hence monkeys are entitled to consider $B$ as some space of ``functions''. When the values of $Z(K)$ are considered as ``functions'' in this way, it turns out that the Kirby slide move (the main move that makes the theory of 3-manifolds a quotient of the theory of links) acts on these ``functions'' essentially by shear transformations. Therefore if one could compute the ``integral'' of $Z(K)$, it would be a 3-manifold invariant. We compute such ``integrals'' in completely combinatorial terms using a formal analog of Feynman diagrams, and call the result ``the Århus integral'' of a rational homology sphere.

Literature guide: The ``monkey's view of algebra'' is not an official name. Nevertheless, the ``monkey PBW'' theorem is stated and proven in [B-N4, Section 5] (using a different language, of course), and the monkey's view of spaces of functions is in [Å2, Section 2]. The above philosophy is presented in detail (alas, again under a different guise) in [Å1], while the proofs that everything works even outside of the African jungles is in [Å2]. Finally, the proof that the resulting invariant is equal to the LMO invariant of [LMO] is in [Å3].

Bibliography

Å

In the Danish alphabet, Å comes after Z.

AF

D. Altschuler and L. Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, to appear in Comm. Math. Phys. See also http://xxx.lanl.gov/abs/q-alg/9603010.

B-N1

D. Bar-Natan, Perturbative Chern-Simons theory, Jour. of Knot Theory and its Ramifications 4-4 (1995) 503-548. See also http://www.math.toronto.edu/~drorbn/LOP.html#pcs.

B-N2

D. Bar-Natan, Weights of Feynman diagrams and the Vassiliev knot invariants, Princeton University preprint, February 1991. See also http://www.math.toronto.edu/~drorbn/LOP.html#Weights.

B-N3

D. Bar-Natan, Perturbative Aspects of the Chern-Simons Topological Quantum Field Theory, Ph.D. thesis, Princeton University, June 1991. See also http://www.math.toronto.edu/~drorbn/LOP.html#thesis.

B-N4

D. Bar-Natan, On the Vassiliev knot invariants, Topology 34 (1995) 423-472. See also http://www.math.toronto.edu/~drorbn/papers/OnVassiliev/.

B-N5

D. Bar-Natan, Vassiliev homotopy string link invariants, Jour. of Knot Theory and its Ramifications 4 (1995) 13-32. See also http://www.math.toronto.edu/~drorbn/LOP.html#Homotopy.

B-N6

D. Bar-Natan, Polynomial invariants are polynomial, Math. Res. Lett. 2 (1995) 239-246. See also http://www.math.toronto.edu/~drorbn/LOP.html#Polynomial.

BS

D. Bar-Natan and A. Stoimenow, The fundamental theorem of Vassiliev invariants, in Proc. of the Århus Conf. Geometry and physics, (J. E. Andersen, J. Dupont, H. Pedersen, and A. Swann, eds.), lecture notes in pure and applied mathematics 184 (1997) 101-134, Marcel Dekker, New-York. See also http://www.math.toronto.edu/~drorbn/LOP.html#Fundamental and http://xxx.lanl.gov/abs/q-alg/9702009.

Bi

J. S. Birman, New points of view in knot theory, Bull. Amer. Math. Soc. 28 (1993) 253-287.

BL

J. S. Birman and X-S. Lin, Knot polynomials and Vassiliev's invariants, Invent. Math. 111 (1993) 225-270.

Bo

R. Bott, Configuration spaces and imbedding problems, in Proc. of the Århus Conf. Geometry and physics, (J. E. Andersen, J. Dupont, H. Pedersen, and A. Swann, eds.), lecture notes in pure and applied mathematics 184 (1997) 135-140, Marcel Dekker, New-York.

BT

R. Bott and C. Taubes, On the self-linking of knots, Jour. Math. Phys. 35 (1994).

Go1

M. Goussarov, A new form of the Conway-Jones polynomial of oriented links, in Topology of manifolds and varieties (O. Viro, editor), Amer. Math. Soc., Providence 1994, 167-172.

Go2

M. Goussarov, On n-equivalence of knots and invariants of finite degree, in Topology of manifolds and varieties (O. Viro, editor), Amer. Math. Soc., Providence 1994, 173-192.

LMO

T. Q. T. Le, J. Murakami and T. Ohtsuki, On a universal quantum invariant of 3-manifolds, Topology 37-3 (1998) 539-574. See also http://www.math.buffalo.edu/~letu/ and http://xxx.lanl.gov/abs/q-alg/9512002.

Po1

S. Poirier, Rationality results for the configuration space integral of knots, Universite de Grenoble I preprint, December 1998. See also http://xxx.lanl.gov/abs/math/9901028.

Po2

S. Poirier, The limit configuration space integral for tangles and the Kontsevich integral, Universite de Grenoble I preprint, February 1999. See also http://xxx.lanl.gov/abs/math/9902058.

Th

D. Thurston, Integral expressions for the Vassiliev knot invariants, Harvard University senior thesis, April 1995. See also http://xxx.lanl.gov/abs/math/9901110.

Va1

V. A. Vassiliev, Cohomology of knot spaces, in Theory of Singularities and its Applications (Providence) (V. I. Arnold, ed.), Amer. Math. Soc., Providence, 1990.

Va2

V. A. Vassiliev, Complements of discriminants of smooth maps: topology and applications, Trans. of Math. Mono. 98, Amer. Math. Soc., Providence, 1992.

Wi

E. Witten, Quantum field theory and the Jones polynomial, Commun. Math. Phys. 121 (1989) 351-399.

Ya

S.-W. Yang, Feynman integral, knot invariant and degree theory of maps, National Taiwan University preprint, September 1997. See also http://xxx.lanl.gov/abs/q-alg/9709029.

Å1

D. Bar-Natan, S. Garoufalidis, L. Rozansky and D. P. Thurston, The Århus integral of rational homology 3-spheres I: A highly non trivial flat connection on $S^3$, Selecta Math., to appear. See also http://www.math.toronto.edu/~drorbn/LOP.html#AarhusI and http://xxx.lanl.gov/abs/q-alg/9706004.

Å2

D. Bar-Natan, S. Garoufalidis, L. Rozansky and D. P. Thurston, The Århus integral of rational homology 3-spheres II: Invariance and universality, Selecta Math., to appear. See also http://www.math.toronto.edu/~drorbn/LOP.html#AarhusII and http://xxx.lanl.gov/abs/math/9801049.

Å3

D. Bar-Natan, S. Garoufalidis, L. Rozansky and D. P. Thurston, The Århus integral of rational homology 3-spheres III: The relation with the Le-Murakami-Ohtsuki invariant, preprint. See http://www.math.toronto.edu/~drorbn/LOP.html#AarhusIII and http://xxx.lanl.gov/abs/math/9808013.

       Time for Tubby Bye Bye

About this document ...

From Astrology to Topology via Feynman Diagrams and Lie Algebras

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.49)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -no_navigation -dir notes notes.tex

The translation was initiated by Dror Bar-Natan on 2002-10-19