Quantum Probability

Dror Bar-Natan, University of Western Ontario, February 13, 2004

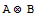
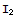
See http://www.math.toronto.edu/~drorbn/Talks/QuantumProbability/UWO-040213.html

We start by loading a necessary Mathematica package, by defininig the tensor product A ⊗ B of two matrices A and B and the 2×2 identity matrix  I _ 2:

In[1]:=

<< LinearAlgebra`MatrixManipulation`

In[2]:=

A_ ⊗ B_ := BlockMatrix[Outer[Times, A, B]] ; I _ 2 = IdentityMatrix[2] ;

Next we define the unit "probability vector" v, and our observables ("random variables")  A _ α and B _ β as tensor products of I _ 2 with some prescribed S _ γ:

In[3]:=

v = 2^(1/2)/2 {0, 1, -1, 0} ; S _ γ_ := (Cos[2 γ] Sin[2 γ] ) ; A _ α_ : ... #946; ⊗ I _ 2 Sin[2 γ] -Cos[2 γ]

In[4]:=

{A _ α // MatrixForm, B _ β // MatrixForm}

Out[4]=

{( Cos[2 α] Sin[2 α] 0 0 ), ( Cos[2 β] 0 ... 2 α] -Cos[2 α] 0 Sin[2 β] 0 -Cos[2 β]

We check that both A _ α and B _ β are (±1)-valued and have zero mean, hence both attain +1 and -1 with 50-50 chance:

In[5]:=

{{Eigenvalues[A _ α], v . A _ α . v}, {Eigenvalues[B _ β], v . B _ β . v}}

Out[5]=

{{{-1, -1, 1, 1}, 0}, {{-1, -1, 1, 1}, 0}}

The A _ α's and the B _ β's commute, hence they have a joint distribution! Indeed,

In[6]:=

A _ α . B _ β == B _ β . A _ α

Out[6]=

True

The A _ α's and the B _ β's are both (±1)-valued, so the probability that they are equal is the expectation value (mean) of (1 + A _ α B _ β)/2:

In[7]:=

p _ eq[α_, β_] := Simplify[(1 + v . A _ α . B _ β . v)/2]

Finally, the following is stricktly impossible, classically speaking:

In[8]:=

{p _ eq[α, β], Outer[p _ eq, {-60 °, 0, 60 °}, {-60 °, 0, 60 °}] // MatrixForm}

Out[8]=

{Sin[α - β]^2, ( 3 3 )} - - ... 3 3 - - 4 4 0

See also N. D. Mermin,  Physics Today 39(4) 38 (1985) and D. Bar-Natan, Foundations of Physics 19(1) 97 (1989).

Converted by Mathematica  (February 12, 2004)