Algebraic Knot Theory Summary

an unproven thesis and an untested principle, appealing but mired with unknowns and known obstractions
(Read: Risks & Opportunities Abound)

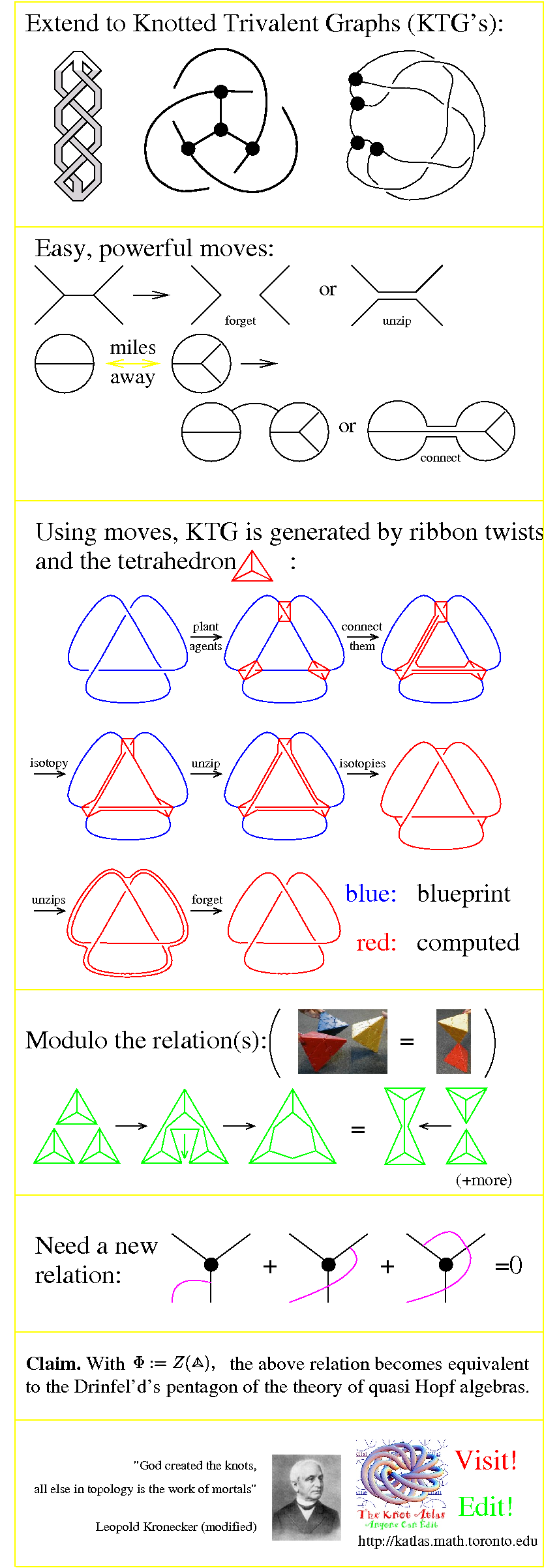
• The Thesis. Every 3D property of knots and link is definable in terms of Knotted Trivalent Graphs.
  • 3D Property.
    1. Having braid index 6.
    2. Having a projection with 23 crossings.
    3. Having an alternating projection.
    4. Bounding a disk in B⁴.
    5. Being algebraic.
    6. Having unknotting number 3.
    7. Bounding a Seifert Surface of genus < 7.
    8. Being a boundary link.
    9. Being a ribbon knot.
    10. Being fibred.
    11. Having a vanishing Alexander polynomial.
  • Definable. Within some given collections of objects, in terms of a finite formula utilizing some operations provided in advance. Examples:
    • In algebra.
    • In strict knot and link theory.
  • Knotted Trivalent Graphs.
• The Principle. Seek a TG-morphism from KTG to algebra.
  • Aside. KTG is finitely presented - to find a TG-morphism you need to make two guesses and carry out three checks. And when you're done, you've rediscovered Drinfel'd's theory of associators.
• A Prime Candidate. The theory of finite type invariants, as studied in Stonhenge.
  • A Sad Truth. Z is practically surjective at bounded degrees for several definable classes of knots (e.g. Ng's arXiv:q-alg/9502017). There are also some bad news about "bounded loop counts" (Garoufalidis-Rozansky arXiv:math.GT/0003187).

• Put Your Name Here.
  • Do the Alexander test case - recover Fox-Milnor (for ribbon knots, A(t)=f(t)f(1/t)).
    • What's in the envelope of the Alexander polynomial, if we're talking about knots or graphs?
    • Control the Alexander associator (see Lieberum's arXiv:math.QA/0204346).
  • Pull something out of Jones' envelope.
  • Find the envelopes of other interesting finite type invariants.
  • Study other internal quotients of the TG-algebra of chord diagrams. There are plenty, even plenty with polynomial behaviour!
  • Formalize and classify such internal quotients.
  • Tame one associator and show it to your friends. (Or be brave and master the theory of multiple ζ-numbers).
  • Complete the Stonhenge story for KTGs.
  • Venture outside of Stonehenge! Surgery quotients?
  • Are fibred knots definable?
  • Are there other interesting definable classes of knots?
  • What's "a TG-algebra"? (See D. Thurston's arXiv:math.GT/0311458). Make precise the sufficiency of the pentagon and the hexagons for KTG.