Colloquium, October 28.
Abstract. In my talk I will display one complicated picture and discuss it at length, finding that it's actually quite simple. Applying a certain 2D TQFT, we will get a homology theory whose Euler characteristic is the Jones polynomial. Not applying it, very cheaply we will get an invariant of tangles which is functorial under cobordisms and an invariant of 2-knots.
Why is it interesting?
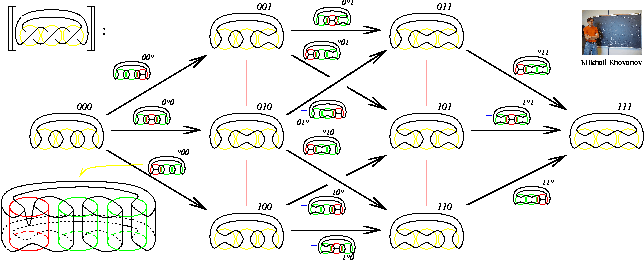
The picture:

Handouts:
MoreFormulas.pdf.
NewHandout-1.pdf,
Transparencies:
Reid2Proof.pdf,
R3Full.pdf,
FrameRack.pdf.
See also my paper Khovanov's
Homology for Tangles and Cobordisms.
Gauge Theory and Topology Seminar (though it's really an algebra talk), October 29
Abstract. We will really see how the Euler characteristic of Khovanov homology comes to be the Jones polynomial; this will take introducing the notion of "trace groups" and generalizing the notion of "Euler characteristic" to be valued in more than just integers or power series. I will then quickly explain all that I know about Khovanov-Rozansky homology which is to HOMFLY like Khovanov homology is to Jones. "Quickly" and "all that I know" correctly indicate that I know too little, and in particular, we don't know how to play the trace groups game in this arena. But even so, the basic Khovanov-Rozansky story is good and involves a novel technique. How come it's not in every book?
Handouts:
TraceGroups.pdf,
idea.jpg,
KRHDefinitions.png,
KRHDefinitions.nb.
See also my paper Khovanov's
Homology for Tangles and Cobordisms and the paper math.QA/0401268
by Khovanov and Rozansky.